La configuración PP

Contenido

1 Simulación de la configuración mínima PP

Simulación de la configuración mínima PP

Capítulo anterior

Índice

Capítulo siguiente

Introducción

En este ejemplo simulamos nuestro primer robot modular, constituido únicamente por la unión de dos módulos de tipo cabeceo. Es la configuración mínima que puede moverse en línea recta. Se conoce bajo el nombre de configuración PP (Pitch-Pitch). El usuario puede mover el robot hacia adelante, atrás o pararlo, por medio del teclado.

Objetivos

Simular la locomoción del robot modular más sencillo
Presentar la técnica de locomoción mediante osciladores sinusoidales

Código

PP_ex/PP.cpp	Programa principal
PP_ex/robot.cpp	Creación y dibujo del robot
PP_ex/parameters.h	Definición de las constantes.
PP_ex/robot.h	Definición de los prototipos de robot.cpp y las estructuras de datos.

Compilación

Todos los ejemplos de este tutorial compilan tecleando "make". Sin embargo se describe a continuación cómo se compila directamente usando el GCC:

g++ -Iinclude -c -o PP_ex/PP.o PP_ex/PP.cpp
g++ -Iinclude -c -o PP_ex/robot.o PP_ex/robot.cpp
g++ -o PP PP_ex/PP.o PP_ex/robot.o libdrawstuff.a -lm -lode -lX11 -lGL -lGLU

Ejecución

Para probar el ejemplo, teclear:

./PP

Además de los mensajes impresos en pantalla por la drawstuff, aparecerá el siguiente menú:

 Keys for controlling the robot: 
 1: Move Backward
 2: Move Forward
 3: Stop
 q: Quit

Por medio de las teclas '1', '2' y '3' el usuario hace que el robot se mueva hacia atrás, adelante o se pare.

Capturas de pantalla

Visualización del robot en tres instantes diferentes:

Pinchar para ampliar

Vídeo

Modelo de robot

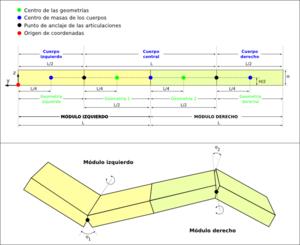
Figura 1:Modelo geométrico de la configuración PP

El modelo geométrico de la configuración PP se muestra en la figura 1. Está compuesta por:

2 Módulos iguales, de dimensiones W x L x H y masa MASS.
3 cuerpos: izquierdo, central y derecho. El izquierdo y el derecho están formados por una geometría de longitud L/2 mientras que el central por la unión de dos, con una longitud de L
4 geometrías: Denominadas geometría izquierda, geometría derecha y las centrales: geometría 1 y 2.
2 articulaciones.

Las posiciones de los elementos con respecto al origen de coordenadas son:

Articulación 1	(0,-L/2, H/2)
Articulación 2	(0,-3L/2, H/2)
Cuerpo izquierdo:	(0,-L/4, H/2)
Cuerpo derecho:	(0, -7L/4, H/2)
Cuerpo central:	(0, -L, H/2).

Las dos geometrías del cuerpo central están desplazadas -L/4 y L/4 a lo largo del eje y

La estructura de datos está definida en el fichero robot.h:

struct MyRobot {
  dJointID joint[2];      //-- Robot joints. 0--> left, 1--> right
  dReal servo_ref_pos[2]; //-- Reference positions for the servos
 
  dBodyID body_left;       //-- This is the body on the left
  dGeomID geom_left;       //-- and its geometry (a box)
 
  dBodyID body_center;    //-- Central body. It has two geometries
  dGeomID geom1;          //-- One in the left and another 
  dGeomID geom2;          //-- in the right
 
  dBodyID body_right;     //-- This is the body on the right 
  dGeomID geom_right;     //-- and its geometry (a box)
};

Modelo de control

Figura 2: Modelo de control para la configuración PP

Para mover este robot usaremos un controlador bioinspirado basado en osciladores sinusoidales que actúan sobre las articulaciones. De esta manera, las posiciones de referencia de los servos están dadas por las ecuaciones:

<math>\varphi_{1}\left(n\right)=A\sin\left(\frac{2\pi}{N}n\right)</math>
<math>\varphi_{2}\left(n\right)=A\sin\left(\frac{2\pi}{N}n+\Delta\phi\right)</math>

donde los parámetros son:

A	Amplitud de las oscilaciones (grados)
<math>\Delta\phi</math>	Diferencia de fase entre el oscilador izquierdo y derecho
N	Número de muestras por ciclo
n	Tiempo discreto
<math>\varphi_{1},\varphi_{2}</math>	Posiciones de referencia en el instante n

Secuencias de movimiento

Figura 3: Secuencia de movimiento para un servo

Las secuencias de movimiento son las tablas que continen las posiciones de referencia para los servos. Se calculan mediante las ecuaciones anteriores. En total se establecen N posiciones de referencia para cada servo (N es el número de muestras). Sólo cuando ambos servos han alcanzado sus posiciones de referencia se establecen las siguientes. Esta es la condición para saltar a la siguiente posición. De esta manera se consigue que los servos estén siempre sincronizados. La denominamos condición de disparo.

Según se mostró en el capítulo anterior, la velocidad del servo es proporcional a la distancia que le queda por llegar hasta la posición de referencia (el error). Según se acerca, la velocidad cada vez es menor y al alcanzarla es de 0. Cuando se aplica este controlador a la locomoción de un robot, el efecto que se observa es que los servos se mueven "a tirones", de una forma brusca. Es debido a que se paran al llegar a la posición de referencia y luego vuelven a arrancar para ir a la siguiente. Para conseguir un movimiento más suave, no se va a esperar a que se alcance exactamente la posición de referencia indicada (ya que al llegar a ella el servo tendrá velocidad 0) sino que se considerará que la a alcanzado cuando se cumpla que: <math>\left|\varphi\left(t\right)-p\right|<ERROR</math>, donde:

<math>\varphi\left(t\right)</math> es la posición instantánea del servo
p: Es la posición de refencia
ERROR: Una constante. Su valor por defecto es de 5 grados.

Es decir, que antes de que el servo se pare, se establece la siguiente posición de referencia.

En la figura 3 se muestra la simulación del ángulo de dobleja de un servo cuando las posiciones de referencia que se introducen son muestras de una sinusoide. El número de muestras N es 8. Se muestran los 8 instantes discretos de tiempo <math>n_{i}</math>

Espacio de control

Una vez establecido el modelo de control basado en generadores sinusoidales, la locomoción del robot se realiza dando valores a los parámetros A y <math>\Delta\Phi</math>. A este nivel el usuario no tiene que saber nada de servos ni de secuencias, simplemente establecer los valores adecuados.

El espacio formado por los parámetros (A,<math>\Delta\Phi</math>) se denomina espacio de control. La diferencia de fase determina la coordinación entre los módulos y la amplitud está relacionada con el paso que da el robot en un ciclo. Cuando el modelo de configuración PP es alámbrico (el parámetro H tiende a 0), la mejor coordinación se obtiene para una diferencia de fase de 110 grados.

El signo de <math>\Delta\Phi</math> determina el sentido de desplazamiento del robot.

Explicación del código

Función Robot_new()

Esta es la función que se encarga de crear el robot. Primero se crea el cuerpo izquierdo, que está compuesto únicamente por una geometría. Tiene de masa MASS/2 y está situado en las coordenadas (0,-L/4,H/2). Sus dimensiones son (W, L/2, H):

pp->body_left = dBodyCreate(world);
dBodySetPosition(pp->body_left, 0.0, -L/4, H/2);
dMassSetBoxTotal (&m, MASS/2, W,L/2,H);
dBodySetMass (pp->body_left,&m);
pp->geom_left = dCreateBox (space, W,L/2, H); 
dGeomSetBody (pp->geom_left,pp->body_left);

A continuación se crea el cuerpo central, de masa MASS, dimensiones (W, L, H) y situado en (0,-L,H/2). Está compuesto por dos geometrías hexaédricas, de dimensiones (W,L/2,H) y desplazadas -L/4 y L/4 del centro de masas del cuerpo:

 pp->body_center=dBodyCreate(world);
 dBodySetPosition(pp->body_center, 0.0, -L, H/2);
 dMassSetBoxTotal (&m, MASS, W,L/2,H);
 dBodySetMass (pp->body_center,&m); 

 pp->geom1 = dCreateBox (space, W,L/2, H); 
 pp->geom2 = dCreateBox (space, W,L/2, H); 
 dGeomSetBody (pp->geom1,pp->body_center);
 dGeomSetBody (pp->geom2,pp->body_center);
 
 dGeomSetOffsetPosition (pp->geom1, 0.0,  L/4, 0.0);
 dGeomSetOffsetPosition (pp->geom2, 0.0, -L/4, 0.0);

Luego se hace lo propio con el cuerpo derecho, de masa MASS/2, dimensiones (W,L/2,H) y situado en (0,-7L/4,H/2):

 pp->body_right = dBodyCreate(world);
 dBodySetPosition(pp->body_right, 0.0, -7*L/4, H/2);
 dMassSetBoxTotal (&m, MASS/2, W,L/2,H);
 dBodySetMass (pp->body_right,&m);
 pp->geom_right = dCreateBox (space, W,L/2, H); 
 dGeomSetBody (pp->geom_right,pp->body_right);

Y por último se crean las dos articulaciones (izquierda y derecha), cuyos puntos de anclaje están en (0, -L/2, H/2) y (0, -3L/2, H/2) respectivamente y su eje de rotación es el eje x (1,0,0):

 //-- Create the left joint
 pp->joint[0]=dJointCreateHinge (world, 0);
 dJointAttach (pp->joint[0],pp->body_left,pp->body_center);
 dJointSetHingeAxis (pp->joint[0], 1,0,0); 
 dJointSetHingeAnchor (pp->joint[0], 0, -L/2, H/2);
 dJointSetHingeParam(pp->joint[0], dParamFMax, TORQUE);
 dJointSetHingeParam(pp->joint[0], dParamVel, 0.0);
   
 //-- Create the right joint
 pp->joint[1]=dJointCreateHinge (world, 0);
 dJointAttach (pp->joint[1],pp->body_center,pp->body_right);
 dJointSetHingeAxis (pp->joint[1], 1,0,0);  //-- Pitch
 dJointSetHingeAnchor (pp->joint[1], 0, -3*L/2, H/2);
 dJointSetHingeParam(pp->joint[1], dParamFMax, TORQUE);
 dJointSetHingeParam(pp->joint[1], dParamVel, 0.0);

Función Robot_Render()

La función de dibujado es muy sencilla. Sólo tiene que establecer la textura, el color y dibujar las cuatro geometrías:

 //-- Set the robot texture
 dsSetTexture (DS_WOOD);
 
 //-- Draw the left module
 dsSetColor (1,1,0);
 drawGeom(pp->geom_left);
 drawGeom(pp->geom1);
   
 //-- Draw the right module
 dsSetColor (0,1,0);
 drawGeom(pp->geom2);
 drawGeom (pp->geom_right);

Función servos_sim()

La simulación de los servos es igual que en el ejemplo anterior, pero ahora se utiliza un bucle para simular los dos servos: el izquierdo y el derecho.

Además, hay que tener en cuenta la condición de disparo. Sólo cuando ambos servos hayan alcanzado sus posiciones de referencia con un error menor a la constante ERROR, se calcularán las siguientes posiciones de referencia.

 int stable=0;
 
 for (int i=0; i<2; i++) {
   dReal pos = dJointGetHingeAngle(pp.joint[i]);
   dReal error = pos - DEG2RAD(pp.servo_ref_pos[i]);
   dReal velocity = -error*KP;
   if (velocity > WMAX) velocity = WMAX;
   if (velocity < -WMAX) velocity = -WMAX;
   dJointSetHingeParam(pp.joint[i], dParamVel, velocity);
   if (fabs(error)<ERROR) stable++;
 }

Al finalizar el bucle se comprueba la condición de disparo. Si se cumple, se llama a la función sequence_generation()

 if (stable==2) {
   sequence_generation();
 }

Función sequence_generation()

Esta función calcula las posiciones de referencia para un instante discreto n a partir de las ecuaciones de los osciladores sinusoidales. Este tiempo n se incrementa.

 pp.servo_ref_pos[0]=A*sin(2*M_PI*n/N);
 pp.servo_ref_pos[1]=A*sin(2*M_PI*n/N + DEG2RAD(PD) );
 n = (n + 1) % N;

Funciones Main y Command()

La función principal es similar a la empleada en el ejemplo del capítulo anterior pero ahora para crear el módulo se invoca a la función Robot_New().

La función command() es la que se ejecuta cuando el usuario presiona una tecla. Según que se haya pulsado '1', '2' ó '3', el robot se moverá hacia adelante, atrás o se parará. El punto de trabajo en el espacio de control es A=60, <math>\Delta\Phi=110</math>. Para una diferencia de fase de 110, el robot se moverá en un sentido y para -110 en el contrario. Cuando la amplitud se establece en 0 grados, el robot permanece en posición horizontal, apoyado sobre el suelo, sin moverse.

 if (cmd=='1') {        //-- Moving forward
   A=60; PD=110;
 }
 else if (cmd=='2') {   //-- Moving backward
   A=60; PD=-110;
 }
 else if (cmd=='3') {   //-- Stop!
   A=0;
 }
 else if (cmd=='q') {
   //-- Finish the simulation and exit
   dsStop();
 }

A este nivel la locomoción de la configuración PP se establece dando valores al punto de trabajo (A,<math>\Delta\Phi</math>). El bucle principal de la simulación se encarga del resto. Además, esta interfaz es la misma para controlar robots virtuales que reales. El software de este nivel simplemente establece el punto de trabajo.

Enlaces