Diseño de piezas con OpenScad II
Contenido
- 1 Ficha
- 2 Introducción
- 3 Descargas
- 4 Aprendiendo más opciones de Openscad
- 4.1 1) Usando un editor mejorado
- 4.2 2) ¡¡¡Las pirámides son cilindros!!!
- 4.3 3) Mis objetos en una cuadrícula, por favor
- 4.4 4) Esferita, esferita, dime donde está la cuadrícula
- 4.5 5) Organiza tus canicas
- 4.6 6) ¡Comparte tus diseños!
- 4.7 7) Tirando tangentes con el operador hull
- 4.8 8) Figuras redondeadas en el plano xy
- 4.9 9) Automatizando con vectores
- 4.10 Apilando 2 objetos
- 4.11 Apilando varios objetos
- 4.12 Mis cubos con curvas, por favor
- 4.13 Objetos condicionales: cilindros redondeados
- 4.14 Redondeados parciales con hull (II)
- 4.15 El operador Minkowski
- 4.16 Estudiando el código compartido por los demás
- 5 Update: Actualizando a Openscad 2014.03
- 6 Objetos 3D a partir de objetos 2D
- 6.1 18 Extruyendo polígonos
- 6.2 19 Extrusión lineal con torsión
- 6.3 20 Extrusión axial
- 6.4 21 Rueda para printbot
- 6.5 22 Extruyendo dibujos con líneas rectas
- 6.6 23 Me gustan las curvas: Extruyendo dibujos con curvas (II)
- 6.7 24 ¡Pon un smiley en tu vida! (III)
- 6.8 25 Extruyendo logos a partir de imagenes
- 6.9 26 Generando polígonos con python
- 7 Para las próximas temporadas de tutoriales ...
- 8 Repositorio
- 9 Licencia
- 10 Sobre este tutorial
- 11 Enlaces
- 12 Noticias
Ficha
- Título: Diseño de piezas con OpenScad II
- Contexto: Continuación del tutorial Diseño de piezas con OpenScad
- Autor: Juan González (Obijuan)
Introducción
Segunda temporada de tutoriales de Openscad. La filosofía es la misma que con los primeros: Intentar que NO SOBREPASEN LOS 3 MINUTOS, de manera que si uno no te gusta, sólo habrás perdido 3 minutos de tu vida.
Nota: Bueno, vale, en algunos vídeos me he pasado de tiempo. Intentaré estar por debajo de 5 minutos siempre :-)
Nota 2: ¡buaaahhhh! En el tutorial 21 me he ido a 10 minutos!
Descargas
| Pendiente... de momento los ejemplos están accesibles desde el repositorio en github |
Aprendiendo más opciones de Openscad
1) Usando un editor mejorado
| Video Tutorial 1 |
|---|
Descripción
El editor de textos que incorpora openscad es muy básico. Vamos a ver cómo podemos utilizar un editor externo
Pasos
Los pasos a realizar son los siguientes:
- Abrir openscad
- Ir a la opción view/hide editor. Con esto dejamos de ver el editor de openscad
- Ir a la opción design/automatic reload and compile
- Salir de openscad. Se quedarán grabadas las estas opciones de manera que la siguiente vez que arranque openscad no hace falta volverlas a activar
Ahora, para editar cualquier programa sólo hay que abrirlo con openscad y luego con el editor de texto que queramos. Cada vez que se graben los cambios, openscad cargará automaticamente ese fichero y lo visualizará.
Configuración del editor kate en Linux
- Instalar kate (sudo apt-get install kate)
- Descargar el fichero openscad.xml
- Copiar el fichero en /usr/share/kde4/apps/katepart/syntax/
sudo cp $HOME/Downloads/openscad.xml /usr/share/kde4/apps/katepart/syntax/
- Dar permiso de lectura al fichero:
sudo chmod a+r /usr/share/kde4/apps/katepart/syntax/openscad.xml
- Ejecutar kate
- Ir a la opción tools > mode > Other > Openscad
Créditos
- El primero que me enseñó esta opción de openscad fue Sergio Vilches
- El fichero con resaltado de sintaxis de kate es obra de Kevin Weekly
2) ¡¡¡Las pirámides son cilindros!!!
| Video Tutorial 2 |
|---|
Descripción
Se muestra cómo con el comando "cylinder" de openscad se pueden crear conos, pirámides y tetraedros
Código
- Fichero: cylindros-2.scad
//-- Cilindro normal. r es el radio, h es la altura *cylinder (r = 20, h = 20, $fn = 100); //-- Cono truncado. r1 radio base inferior, r2 radio de la base superior *cylinder (r1 = 20, r2 = 10, h = 20, $fn = 100); //-- Cono *cylinder (r1 = 20, r2 = 0, h = 20, $fn = 100); //-- Piramide de base hexagonal *cylinder (r1 = 20, r2 = 10, h = 20, $fn = 6); //-- Piramide *cylinder (r1 = 20, r2 = 0, h = 20, $fn = 4); //-- Tetraedro cylinder (r1 = 20, r2 = 0, h = 20, $fn = 3);
3) Mis objetos en una cuadrícula, por favor
| Video Tutorial 3 |
|---|
Descripción
Ejemplo de organización de 6 objetos en una cuadrícula virtual paramétrica. Más adelante esta idea se desarrollará y refinará
Código
- Fichero: cuadricula-1.scad
//-- Dimensiones de los cuadros de la cuadricula
d = 60;
//-- Centrar la cuadricula (opcional)
translate([-2*d / 2, -d / 2, 0]) {
//-- Punto: 0, 0
translate([0, 0, 0]) cylinder (r = 20, h = 20, $fn = 100);
//-- Punto: 1, 0
translate([d, 0, 0]) cylinder (r1 = 20, r2 = 10, h = 20, $fn = 100);
//-- Punto: 2, 0
translate([2*d, 0, 0]) cylinder (r1 = 20, r2 = 0, h = 20, $fn = 100);
//-- Punto: 0, 1
translate([0, d, 0]) cylinder (r1 = 20, r2 = 10, h = 20, $fn = 6);
//-- Punto: 1, 1
translate([d, d, 0]) cylinder (r1 = 20, r2 = 0, h = 20, $fn = 4);
//-- Punto: 2, 1
translate([2*d, d, 0]) cylinder (r1 = 20, r2 = 0, h = 20, $fn = 3);
}
4) Esferita, esferita, dime donde está la cuadrícula
| Video Tutorial 4 |
|---|
Descripción
Aprender a crear esferas. Ejemplo de cómo visualizar una cuadrícula.
Código
Fichero: esfera-cuadricula.scad
//-- Ejemplo de uso de esferas para visualizar una cuadrícula
//-- de N x N cuadros
//-- Tamaño de cada cuadro
d = 30;
//-- Radio de las esferas en la cuadrícula
r = 2;
//-- Número de cuadros (N x N)
N = 10;
//-- Tamaño total de la cuadrícula
size = N * d;
//-- Dibujar la cuadricula
translate([-size / 2, -size / 2, 0]) //-- Centrar cuadricula
for (ix = [0:N]) //-- Esferas en eje x
for (iy = [0:N]) //-- Esferas en eje y
//-- Posicionar la esfera en punto (ix, iy)
translate([ix * d, iy * d, 0])
sphere(r = r, $fn=20);
//-- Objeto ejemplo en punto (2, 2): una esfera roja
translate([2 * d, 2 * d, 0])
color("red")
sphere(r = 15, $fn = 20);
//-- Objeto ejemplo en punto (-3, -4): un cubo azul
color("blue")
translate([-3 * d, -4 * d, 0])
cube([20, 20, 20], center = true);
5) Organiza tus canicas
| Video Tutorial 5 |
|---|
Descripción
Ejemplo de diseño de una pieza paramétrica para organizar las canicas
Código
- Fichero: porta-canicas.scad
//-- Organizador de canicas paramétrico
//-- Número de canicas
N = 3;
//-- Diametro de las canicas
dc = 16;
//-- Tamaño de cada cuadro
d = dc + 3;
//-- Tamaño total de la cuadrícula
size = (N-1) * d;
//-- Tamaño de la caja donde están las canicas
size_box = N * d;
h_box = dc / 2 + 1;
difference() {
//-- Caja de las canicas
translate([0, 0, -h_box / 2])
cube([size_box, size_box, h_box], center = true);
//-- Canicas
translate([-size / 2, -size / 2, 0]) //-- Centrar canicas
for (ix = [0:N-1])
for (iy = [0:N-1])
//-- Posicionar la canica en punto (ix, iy)
translate([ix * d, iy * d, 0])
sphere(r = dc/2, $fn=20);
}
6) ¡Comparte tus diseños!
| Video Tutorial 6 |
|---|
Descripción
Una vez terminado un diseño... ¡Compártelo! Es la manera de que el conocimiento esté disponible para todos y que podamos mejorar.
Como ejemplo, esto son los sitios donde he compartido el organizador de canicas:
- En mi wiki personal
- El código lo subo a github. Es un repositorio y permite que otros aporten sus modificaciones fácilmente
- También lo he publicado en Fabfabbers
- y en Youmagine
- El repositorio más antiguo es Thingiverse, aunque yo lo he dejado de usar.
7) Tirando tangentes con el operador hull
| Video Tutorial 7 |
|---|
Descripción
El comando hull crea el objeto convexo mínimo que incluye otros objetos indicados. Se muestra su uso para construir una pieza en la que es necesario crear las tangentes entre dos cilindros.
Código
- Fichero: tirando-tangentes.scad
//-------- Parametros de la pieza
r1 = 25; //-- Radio cilindro 1
r2 = 10; //-- Radio cilindro 2
th = 5; //-- Grosor
//-- Distancia entre los centros de los cilincros
d = r1 + r2 + 10;
//-- Crear el objetco convexo minimo que contiene ls dos
//-- cilindros
hull() {
//-- Cilindro 1
translate([-d/2, 0, 0])
cylinder(r = r1, h = th, center = true, $fn = 50);
//-- Cilincro 2
translate([d/2, 0, 0])
cylinder(r = r2, h = th, center = true, $fn = 50);
}
8) Figuras redondeadas en el plano xy
| Video Tutorial 8 |
|---|
Descripción
Ejemplo de cómo se pueden hacer objetos con las aristas verticales redondeadas, usando el comando hull
Código
- Fichero: cubo-redondeado.scad
//-- Parametros de la caja
lx = 50; //-- Longitud en eje x
ly = 40; //-- Longitud en eje y
r = 5; //-- Radio del redondeo de las esquinas
h = 10; //-- Altura
//-- Coordenadas del cilindro del primer cuadrante
cx = lx/2 - r;
cy = ly/2 - r;
//-- Posicion de los 4 cilindros de las esquinas
P1 = [cx, cy, 0];
P2 = [-cx, cy, 0];
P3 = [-cx, -cy, 0];
P4 = [cx, -cy, 0];
//-- Obtener el menor objeto convexo que contiene
//-- los 4 cilindros
hull() {
translate(P1)
cylinder(r = r, h = h, center = true, $fn = 20);
translate(P2)
cylinder(r = r, h = h, center = true, $fn = 20);
translate(P3)
cylinder(r = r, h = h, center = true, $fn = 20);
translate(P4)
cylinder(r = r, h = h, center = true, $fn = 20);
}
9) Automatizando con vectores
| Video Tutorial 9 |
|---|
Descripción
Creación de objetos redondeados a partir de un número genérico de cilindros. Las posiciones de los cilincros se guardan en un vector (array). Usando un bucle for se recorren y se colocan automáticamente los cilindros. Luego se aplica hull para generar el objeto convexo mínimo que contiene todos los cilindros.
Código
- Fichero: poligonos-redondeados.scad
//-- Parametros
r = 5; //-- Radio del redondeo de las esquinas
h = 10; //-- Altura
//-- Coordenadas del cilindro del primer cuadrante
cx = 20;
cy = 15;
//-- Vector de puntos, con las posiciones de los cilindros
POINT = [
[cx, cy, 0], //-- Punto 0
[-cx, cy, 0], //-- Punto 1
[-cx, -cy, 0], //-- Punto 2
[cx, -cy, 0], //-- Punto 3
[2*cx, 0, 0], //-- Punto 4
[0, 1.5*cy, 0], //-- Punto 5
[0,0,h], //-- Punto 6
];
//-- Obtener el menor objeto convexo que contiene
//-- los cilindros situados en los puntos indicados en
//-- el vector POINT
hull() {
//-- Dibujar cada cilindro en su posicion correspondiente
for (pos = POINT)
translate(pos)
cylinder(r = r, h = h, center = true, $fn = 20);
}
Apilando 2 objetos
| Video Tutorial 10 |
|---|
Descripción
Apilar 2 objetos es fácil... pero usando vectores es mucho más fácil aún y el código se mantiene mejor
Código
- Fichero: apilando-2-cajas.scad
//-- Definiciones para acceder a las componentes X,Y,Z //-- Aunque las definimos todas, en este ejemplo solo //-- accedemos a la componente Z de los cubos X = 0; Y = 1; Z = 2; //-- Dimensiones de los cubos. Se pueden cambiar por el usuario //-- Todo se recalculara para que B esté siempre encima de A A = [30, 30, 10]; B = [10, 10, 30]; //-- Calcular la posicion de B para que este encima de A posB = [0, 0, B[Z]/2 + A[Z]/2]; //---- Construccion de la figura a partir de los datos calculados! //-- Poner el cubo B encima del A //-- Poner el cubo A (es la base) cube(A, center = true); //-- Cubo B, encima de A translate(posB) cube(B, center = true);
Apilando varios objetos
| Video Tutorial 11 |
|---|
Descripción
Se propone como ejercicio modificar el ejemplo del tutorial anterior para apilar 4 objetos
Código
- Fichero: apilando-varias-cajas.scad
//-- Definiciones para acceder a las componentes X,Y,Z //-- Aunque las definimos todas, en este ejemplo solo //-- accedemos a la componente Z de los cubos X = 0; Y = 1; Z = 2; //-- Dimensiones de los cubos. Se pueden cambiar por el usuario //-- Todo se recalculara para que todos los cubos esten apilados A = [30, 30, 10]; B = [10, 10, 30]; C = [6, 6, 10]; D = [3, 3, 3]; //-- Calcular las posicion de los cubos para que esten apilados posB = [0, 0, B[Z]/2 + A[Z]/2]; posC = posB + [0, 0, C[Z]/2 + B[Z]/2]; posD = posC + [0, 0, D[Z]/2 + C[Z]/2]; //---- Construccion de la figura a partir de los datos calculados! //-- Poner el cubo A (es la base) cube(A, center = true); //-- Cubo B, encima de A translate(posB) cube(B, center = true); //-- Poner el cubo C encima del B translate(posC) cube(C, center = true); //-- Poner el cubo D encima del C translate(posD) cube(D, center = true);
Mis cubos con curvas, por favor
| Video Tutorial 12 |
|---|
Descripción
Crear un cubo con todas las aristas redondeadas es muy fácil. Basta con colocar esferas en cada uno de los vertices y aplicar el comando hull. Para que el cubo tenga las mismas dimensiones que el equivalente sin redondear, hay que calcular las coordenadas de las 8 esferas.
Código
- Fichero: cubo-redondeado-3d.scad
//-- Constantes para acceder a las coordenadas X,Y,Z de los vectores
X = 0;
Y = 1;
Z = 2;
//-- Parámetros del cubo redondeado
r = 4; //-- Radio de las curvas
A = [30, 30, 20]; //-- Dimensiones del cubo
//-- Calcular las coordenadas en funcion de los parametros del user
a = (A - [2*r, 2*r, 2*r])/2;
//-- Obtener las coordenadas. Es un atajo para no escribir tanto
x = a[X];
y = a[Y];
z = a[Z];
//-- Calcular los vertices del cubo
vertice = [
[x, y, z],
[-x, y, z],
[-x, -y, z],
[x, -y, z],
[x, y, -z],
[-x, y, -z],
[-x, -y, -z],
[x, -y, -z],
];
//-- Cubo de comprobacion. Mismas dimensiones pero sin
//-- redondear. El redondeado debe tener las mismas dimensiones
%cube(A, center = true);
//-- Dibujar el cubo redondeado. Se coloca en cada vertice una
//-- esfera de radio r y se aplica el operador hull
hull()
for (pos = vertice)
translate(pos)
sphere(r = r, $fn = 20);
Objetos condicionales: cilindros redondeados
| Video Tutorial 13 |
|---|
Descripción
Crearemos un objeto condicional denominado rcylinder. En función del parámetro both, se dibuja bien un cilindro con ambas tampas redondeadas, o bien sólo con la superior. También la translación aplicada dependerá del valor del parámetro center.
Código
- Fichero: cilindro-redondeado.scad
//-- Cilindro redondeado en las tapas
//-- Parametros:
//-- r: radio del cilindro
//-- h: Altura del cilindro
//-- center : [true, false], centrar el cilindro
//-- both: [true, false]
//-- true: Redondear ambas tapas (superior e inferior)
//-- false: solo se redondea la tapa superior
module rcylinder(r = 4,
h = 20,
center = false,
both = false, $fn = 30)
{
//-- Calcular la altura del cilindro interior
//-- Si redondeo por las dos tapas, vale h - 2*r
//-- si solo una tapa entonces h - r
hc = (both == true) ? h - 2 * r : h - r;
//-- Calcular la traslacion para centrar el cilindro
posc = (center == true) ? 0 : h/2;
//-- Aplicar traslaciopn para el centrado
translate([0, 0, posc])
//-- Cilindro con ambas tapas redondeadas
//-- Se pone un cilindro de altura hc y una esfera
//-- en la parte superior y otra en la inferior
if (both == true) {
cylinder(r = r, h = hc, center = true, $fn = $fn);
//-- Esferas superior e inferior
for (i = [-1, 1])
translate([0, 0, i * hc / 2])
sphere(r = r);
}
//-- Cilindro con tapa superior redondeada
else
//-- Centrar la figura
translate([0, 0, -h/2]) {
//-- Cilindro + esfera
cylinder(r = r, h = hc, $fn = $fn);
translate([0, 0, hc]) sphere(r = r, $fn = $fn);
}
}
//-- Parametros para los ejemplos
r = 5;
h = 30;
center = false;
$fn = 30;
//-- Cilindro normal
translate([-3*r, 0, 0])
cylinder(r = r, h = h, center = center, $fn = $fn);
//-- Cilindro con tapa superior redondeada
rcylinder(r = r, h = h, both = false, center = center, $fn = $fn);
//-- Cilindro con ambas tapas redondeadas
translate([3*r, 0, 0])
rcylinder(r = r, h = h, both = true, center = center, $fn = $fn);
Redondeados parciales con hull (II)
| Video Tutorial 14 |
|---|
Descripción
Ejemplo de cómo hacer figuras con diferentes terminaciones en las aristas. Según cómo combinemos los objetos con hull, conseguimos aristas en 90 grados, en chaflán o redondeadas
Código
- Ficheros:
- redondeos_parciales.scad
- Cylindros redondeados: rcylinder.scad
use <rcylinder.scad>
X = 0;
Y = 1;
Z = 2;
//-- Parametros del cubo
size = [20, 20, 10];
r = 2;
//-- Calcular las coordenadas de la esquina del cuadrante 1
xc = size[X]/2 - r;
yc = size[Y]/2 - r;
zc = size[Z]/2;
//-- Tamaño de las columnas cuadradas
col_size = [2 * r, 2 * r, size[Z]];
//-- Posiciones de las columnas
vertex = [
[xc, yc, 0],
[-xc, yc, 0],
[-xc, -yc, 0],
[xc, -yc, 0],
];
//-- Ejemplo 1: Modificacion de las aristas verticales
module example1()
{
hull() {
for (v = [0:1])
translate(vertex[v])
cube(col_size, center = true);
//cylinder(r = r, h = size[Z], center = true, $fn = 4);
translate(vertex[2])
cylinder(r = r, h = size[Z], center = true, $fn = 50);
translate(vertex[3])
cylinder(r = r, h = size[Z], center = true, $fn = 4);
}
}
//-- Ejemplo 2: Modificacion de las aristas horizontales y verticales
module example2()
{
hull() {
for (v = [0:3])
translate(vertex[v])
//cylinder(r = r, h = size[Z], center = true, $fn = 50);
rcylinder(r = r, h = size[Z], both = false, center = true, $fn = 40);
//rcylinder(r = r, h = size[Z], both = true, center = true, $fn = 40);
}
}
//-- Ejemplos para probar
example1();
//example2();
El operador Minkowski
| Video Tutorial 15 |
|---|
Descripción
Utilización del operador Minkowski para redondear tanto las aristas verticales como horizontales de un objeto no convexo
Código
- Ficheros:
- minkowski.scad
- Cylindro redondeado: rcylinder.scad
use <rcylinder.scad>
X = 0;
Y = 1;
Z = 2;
size = [20, 20, 10];
r = 2;
//-- Pieza de ejemplo, a la que aplicar Minkowski
module pieza()
{
cube(size, center = true);
translate([10,10,0])
cube(size, center = true);
}
//-- Aplicar Minkowski a la pieza, usando diferentes objetos
minkowski() {
pieza();
cylinder(r = r, h = 1, center = true, $fn = 10);
//sphere(r = r, $fn = 10);
//rcylinder(r = r, h = 2 * r, both = false, center = true, $fn = 10);
}
// Pieza original, para compararla con la conseguido con minkowski
*pieza();
//-- La otra pieza utilizada con minkowski
*color("red")
translate([-size[X]/2, 0, size[Z]/2])
cylinder(r = r, h = 1, center = true, $fn = 10);
//sphere(r = r, $fn = 10);
//rcylinder(r = r, h = 2 * r, both = false, center = true, $fn = 10);
Estudiando el código compartido por los demás
| Video Tutorial 16 |
|---|
Descripción
La mejora manera de aprender openscad es ver el código de las piezas creadas por otros. Esto es lo grande de los proyectos libres: se tiene acceso a "cómo están hechos", para poder aprender de ellos, modificarlos y mejorarlos.
Algunos proyectos interesantes diseñados con openscad son:
- MCAD : Biblioteca de compoentes: engranajes, motores, servos, tornillos, tuercas...
- Prusa i3: Impresora 3D modelo Prusa i3
- PowerCode: Impresora 3D, modelo PowerCode, derivada de la Prusa i3
- Cyclone: Fresadora imprimible, para hacer circuitos impresos
- Miniskybot Miniskybot: Robot imprimible, para aprender robótica
- REPYZ: Módulos imprimibles para hacer robots de tipo gusano/serpiente
- http://www.openscad.org/cheatsheet/: Chuleta con todos los comandos de openscad. ¡Imprescindible!
Código
- Ficheros:
- 01-MCAD.zip. Biblioteca MCAD
- Prusa3.zip. La Prusa i3
- 03-Code.zip. La Powercode
- 04-cyclone.zip. La Cyclone PCB factory
- 05-miniskybot.zip. El printbot Miniskybot
- 06-REPYZ.zip. Módulos imprimibles
- openscad-cheatsheet.pdf (Chuleta para openscad)
Update: Actualizando a Openscad 2014.03
17 Probando el nuevo Openscad 2014.03
| Video Tutorial 17 |
|---|
Descripción
Se acaba de liberar una nueva versión de openscad: la 2014.03. A partir de ahora es la que se utilizará para los tutoriales. Algunas de las mejoras que incluyen son:
- Editor con resaltado de sintáxis
- Parámetro d para estableder el diámetro en cilindros, esferas y círculos
- Recursividad
Código
- Fichero: zigurat.scad
Ejemplo de una figura recursiva:
//-- Ejemplo de figura recursiva
//-- Piramide escalonada
//-- Utilizar Openscad 2014.03 o superior
//-- Parametros
step = 3; //-- Altura de cada nivel
min = 5; //-- Dimensiones de la parte superior (ultimo nivel)
//-- Modulo recursivo
//-- n: Numero de niveles de la piramide
module zigurat(n)
{
//-- Terminacion: en el nivel uno se situa el cubo superior (pequeño)
if (n <= 1) {
cube([min, min, step], center = true);
}
else {
//-- Dibujar el cubo del nivel n
cube([n * min, n * min, step], center = true);
//-- Colocar encima una piramide de n-1 niveles (recursion)
translate([0, 0, step])
zigurat(n - 1);
}
}
//-- Piramide de 10 niveles
zigurat(10);
Objetos 3D a partir de objetos 2D
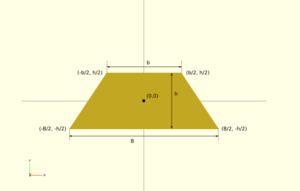
18 Extruyendo polígonos
| Video Tutorial 18 |
|---|
Descripción
Otra forma de diseñar objetos 3D es mediante la creación de polígonos que se extruyen linealmente convirtiéndolos en objetos 3D
Código
- Ficheros:
//-- Parametros del trapecio
B = 40; //-- Base larga
b = 20; //-- Base corta
h = 15; //-- Altura
//-- Rotar prisma para apoyarlo en plano xy
rotate([90, 0, 0])
//-- Extrusion lineal del trapecio
linear_extrude(height = 80, center = true)
//-- Trapecio
polygon(points = [
[-B/2, -h/2],
[-b/2, h/2],
[b/2, h/2],
[B/2, -h/2]
]);
19 Extrusión lineal con torsión
| Video Tutorial 19 |
|---|
Descripción
A la extrusión lineal se le puede añadir torsión con el parámetro twist. Esto permite crear figuras "retorcidas", así como hélices
Código
- Ficheros:
//-- Extrusion lineal con torsion de un rectangulo
translate([-50, 0, 0])
linear_extrude(height = 50, twist = 90, $fn = 100)
square([40,20], center = true);
//-- Extrusion lineal con torsion de un poligono
//-- Triangulo
translate([0, 0, 0])
linear_extrude(height = 50, twist = 120, $fn = 100)
circle(d = 40, $fn = 3);
//-- Hexagono
translate([50, 0, 0])
linear_extrude(height = 50, twist = 120, $fn = 100)
circle(d = 40, $fn = 6);
//-- Circulo
translate([100, 0, 0])
linear_extrude(height = 50, twist = 2*360)
translate([15, 0, 0])
circle(d = 20, center = true);
20 Extrusión axial
| Video Tutorial 20 |
|---|
Descripción
Generación de superficies de revolución usando la extrusión axial. Ejemplos: toro y toroides
Código
- Ficheros:
//-- Parametros del toroide
ri = 10;
ds = 10;
//-- Toroide, de seccion un hexagono
*rotate_extrude($fn = 100)
translate([ds/2 + ri, 0, 0])
circle(d = ds, $fn = 6);
//-- Toroide, cuya seccion es la la union de
//-- varios objetos 2D
rotate_extrude($fn = 100)
translate([ds/2 + ri, 0, 0]) {
translate([ds/2, 0, 0])
circle(d = ds);
square([ds,ds], center = true);
}
21 Rueda para printbot
| Video Tutorial 21 |
|---|
Descripción
Diseño de una rueda para un printbot (robot imprimible) utilizando extrusión axial
Código
- Ficheros:
//-- Parametros de la rueda
di = 50; //-- Diametro interno de la junta torica
ds = 3; //-- Diametro de la junta torica
h = ds + 2; //-- Grosor de la rueda
//-- Parametros calculados
d = di + 2 * ds; //-- Diametro rueda
r1 = d / 2; //-- Radio de la rueda
r2 = ds / 2; //-- Radio de la junta toria
//-- Seccion de la rueda
module section()
{
difference() {
translate([r1 / 2, 0, 0])
square([r1, h], center = true);
//-- Para alojamiento circular
*translate([r1, 0, 0])
circle(d = 3, $fn = 20);
//-- Para alojamiento triangular
translate([r1 - r2, 0, 0])
polygon(points = [[0, 0],
[r2 + 1, r2 + 1],
[r2 + 1, -r2 - 1],
]);
}
}
//-- Junta torica
module junta()
{
rotate_extrude($fn = 100)
translate([r1, 0, 0])
circle(d = ds);
}
//-- Rueda
difference() {
rotate_extrude(convexity = 10, $fn = 100)
section();
//-- Eje de la rueda
cylinder(d = 3, h = h + 10, center = true, $fn = 20);
}
color("grey")
junta();
22 Extruyendo dibujos con líneas rectas
| Video Tutorial 22 |
|---|
Descripción
Openscad puede importar figuras almacenadas en archivos .dxf. Pero estas figuras sólo pueden tener líneas rectas (dxf con curvas no se pueden importar). Para crear figuras usamos programas de diseño 2d, como por ejemplo el Inkscape, que es software libre y multiplataforma. Estas figuras se exportan a formato .dxf y luego se importan en openscad usando el comando import.
Código
- Ficheros:
- extruyendo_dxf_1.scad. Ejemplo en openscad
- flecha.dxf. Fichero 2d con la flecha, en formato dxf
- flecha.svg. Fichero 2d con el dibujo original, en formato vectorial SVG. Es el que se abre con inkscape
linear_extrude(height = 10)
import("flecha.dxf");
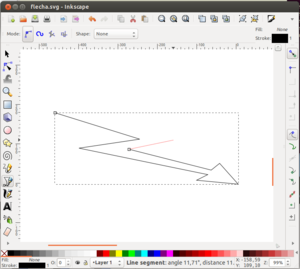
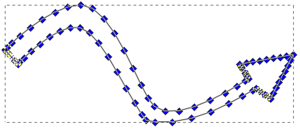
23 Me gustan las curvas: Extruyendo dibujos con curvas (II)
| Video Tutorial 22 |
|---|
Descripción
También es posible extruir objetos en 2d con curvas, pero primero es necesario convertirlos a segmentos rectos. Utilizaremos el inkscape para generar una flecha curva, con curvas de bezier. Al editarla y seleccionar todos los puntos, veremos dos tipos: los puntos normales y los que tienen 2 tiradores que nos permiten cambiar la curvatura:
El primer paso seŕa insertar más puntos, para "discretizar" las curvas en segmentos rectos. Con todos los puntos seleccionados (en azul), pulsaremos el botón "+".
| Botón para añadir más puntos (click para ampliar) |
Cada vez que se pulsa aparecerán nuevos puntos entre cada dos. Apretarlo 3 ó más veces, según la resolución que se quiera.
Ahora apretamos este botón para convertir todos los puntos en normales, y que las curvas sean segmentos en vez de curvas de bezier:
| botón para convertir todos los tramos en segmentos rectos (click para ampliar) |
Y ya no deben aparecer tiradores en los puntos. El objeto está formado sólo por segmentos rectos. Está listo para importarlo en openscad y poder extruirlo!
Código
- Ficheros:
- extruyendo_objetos-2.scad. Ejemplo en openscad
- flecha-curva.dxf. Flecha curvada en DXF
- flecha-curva.svg. Flecha curvada en SVG, para editar con Inkscape
linear_extrude(height = 10)
import ("flecha-curva.dxf");
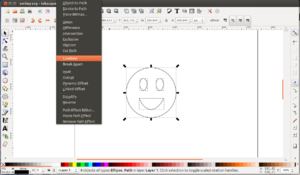
24 ¡Pon un smiley en tu vida! (III)
| [ Video Tutorial 23] |
|---|
Descripción
El smiley está compuesto de 3 círculos y un polígono con curvas de bezier (la sonrisa). Una vez hecho se combinan todos los ejemplos en uno único utilizando la opción path/combine
Se convierte en un objeto hecho sólo con curvas de bezier y rectas.
A continuación hacemos lo mismo que en los tutoriales anteriores: seleccionar todos los puntos para añadir más y convertirlos en líneas rectas
El objeto final formado sólo por puntos normales y líneas rectas
Código
- Ficheros:
- smiley.scad. Ejemplo en openscad
- smiley.dxf. Smiley en dxf
- smiley.svg. Smiley en SVG
linear_extrude(height = 10)
import("smiley.dxf");
25 Extruyendo logos a partir de imagenes
| [ Video Tutorial 22] |
|---|
| [[|thumb|300px| (click para ampliar)]] | [[|thumb|300px| (click para ampliar)]] |
Descripción
obijuan academy
Código
- Ficheros:
- []
26 Generando polígonos con python
| [ Video Tutorial 22] |
|---|
| [[|thumb|300px| (click para ampliar)]] | [[|thumb|300px| (click para ampliar)]] |
Descripción
star
Código
- Ficheros:
- []
Para las próximas temporadas de tutoriales ...
- Operaciones: Escalar, simetrías
- Creando tus propias transformaciones
- Cuadricula: grid
- Using libraries: write
- Obiscad: roudend cube
- Obiscad: Vectors
- Obiscad: beveling and reinforcements
- attach
- MCAD library
Repositorio
Los ficheros fuentes están en este repositorio:
Licencia
| |
Sobre este tutorial
Este tutorial está realizado exclusivamente usando herramientas libres.
|
Enlaces
- http://www.thingiverse.com/thing:29505: Resaltado de sintaxis en kate para Openscad
Noticias
- 11/Marzo/2014: Actualización a Openscad 2014.03. Todos los tutoriales a partir de ahora se harán con esta versión
- 8/Marzo/2014: Tutorial 16: Aprendiendo del código compartido por los demás. Fin de la primera sección
- 25/Dic/2013: Tutorial 1) Usando un editor externo
- 24/Dic/2013: Comenzada la página
|
|
Proyecto Clone wars: Construye tu impresora 3D opensource! |
 |
Proyecto RepRap: Impresoras 3D auto-replicantes. El origen de la revolución de las impresoras 3D opensource |
 |
Obijuan Academy, Tu academia rebelde! ;-) |