Obiscad

[[|thumb|200px|]]

Introducción

Biblioteca de Módulos y objetos en Openscad para facilitar el diseño.

Componentes

Bcube.scad: Cubos biselados

Más información

Cubo biselado con mismo radio pero diferentes resoluciones (click para ampliar)	Pieza hecha a partir de cubos biselados (click para ampliar)
(click para ampliar)	Cubo biselado, con vaciado interior biselado también (click para ampliar)

Vector.scad: Vectores

22 vectores apuntando a diferentes direcciones (click para ampliar)	Probando los vectores y la orientación de un elemento (click para ampliar)
Boceto de robot junto con sus sistemas de referencia, y proyección sobre plano z=0 (click para ampliar)	Cinemática del robot (click para ampliar)

Introducción

Librería para la visualización de vectores y sistemas de referencia. Incluye también el operador orientate() para orientar cualquier pieza según la dirección dada por un vector. Esta librería es especialmente útil para el diseño de robots y estudio de sus cinemáticas, así como para facilitar el diseño de piezas complejas mediante la visualización de vectores auxiliares o sistemas de referencia.

API

• vector(v, l, l_arrow): Dibujar el vector v. l_arrow es la longitud de la flecha. Hay dos modos de dibujo:
  • Modo 1: Cuando el parámetro l es 0, v especifica el vector cartesiado. Se dibuja un vector que va desde el origen y que tiene su punta en las coordenadas indicadas por v
  • Modo 2: Cuando l es distinto de 0, se dibuja un vector en la misma dirección que v, con una longitud de l
  • Ejemplos de uso:

vector([10,20,30]);       //-- Dibujar vector cartesiano
vector([10,20,30],l=50);  //-- Dibujar un vector en la misma dirección que el anterior, pero de longitud 50

• frame(l,l_arrow): Dibujar un sistema de referencia con 3 vectores de longitud l. El parámetro l_arrow indica la longitud de las flechas.
  • Ejemplo:

frame(l=10);

• orientate(v,roll): Operador para orientar cualquier objeto según la dirección dada por v, y rotado un ángulo roll alrededor del eje definido por v
  • Ejemplo:

orientate([1,1,1]) cube([10,10,10])

Dibujar un cubo de 10 de arista y orientarlo en la dirección dada por el vector [1,1,1]

Attach.scad: uniendo piezas

Fig. 1: Parte principal (cuerpo) en la que se han definido 2 connectores (click para ampliar)	Fig. 2: Parte secundaria. Se ha definido 1 conector (click para ampliar)
Fig. 3: Parte principal con dos piezas en sus conectores (click para ampliar)	Fig. 4: La pieza secundaria y el objeto final (click para ampliar)
Fig. 5: Cambio en los ángulos de los conectores (click para ampliar)	Fig. 6: Misma figura, pero en modo no-debug (click para ampliar)

Introducción

El operador attach permite conectar dos piezas en las que se han definido conectores. Hace que el código sea más legible y fácil de entender.

Ejemplo

Partimos de la pieza principal, que en este ejemplo usaremos un cubo. Queremos unir al cubo otras dos piezas, una en la parte superior y otra en la izquierda. Primero definimos los conectores: son los elementos donde se conectarán las piezas.

Un conector consta de 3 componentes: El punto de anclaje, el eje de unión y el ángulo de giro. Para nuestro ejemplo definiremos los dos conectores c1 y c2 así:

//--     punto     eje    ángulo
c1 = [ [0,0,10],  [0,0,1],  20 ]; 
c2 = [ [-10,0,0], [-1,0,0],-30 ];

Para hacerlo más fácil, podemos invocar al comando connect() para verlos gráficamente junto con nuestra pieza:

connector(c1);
connector(c2);

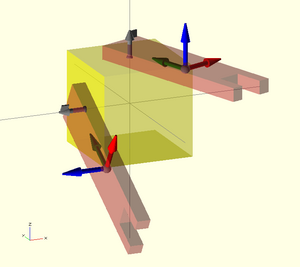
El resultado se muestra en la figura 1. A continuación hacemos lo mismo para otra pieza. En esta solo definimos el conector a:

a = [ [0, 2,2], [0,0,1], 0 ];

Para "depurar" podemos ver tanto el conector como el sistema de referencia de la piza (Figura 2).

Por último, ya podemos unir las piezas secundarias al cuerpo usando attach:

attach(c1,a) mi_pieza();
attach(c2,a) mi_pieza();

¡Y ya está! El código queda muy limpio y fácil de entender. Si ahora cambiamos los ángulo de los connectores (tercera componente) ocurre lo que se muestra en las figuras 5 y 6.

API

• connector(c) : Representar en pantalla el conector c. Se muestras sus tres componentes: una esfera para indicar el punto de anclaje, un vector para el eje de la unión y una marca en la cabeza del vector para el ángulo de giro.
• attach(c1,c2) mi_modulo(); : Se une "mi_modulo()" definido por el conector c2 con el conector c1 del cuerpo principal

Bevel.scad: Biselando lados y añadiendo refuerzos

Fig. 1: Colocando los conectores para biselar el borde de un cubo (click para ampliar)

Fig. 2: Pieza cóncava colocada. ¡Listo para biselar! (click para ampliar)	Fig. 3: ¡La arista está redondeada! (click para ampliar)
Fig. 4: Una caja con aristas y segmentos de aristas biselados (click para ampliar)

Introducción

Hay dos operaciones que se realizan con mucha frecuencia en nuestros diseños: el biselado de los bordes tanto interiores como exteriores. Con el biselado de los exteriores logramos redondear las aristas y que los bordes no estén afilados. Con el biselado interior se consigue reforzar las uniones entre piezas ortogonales.

Ejemplo 1

Partimos de una caja. Queremos biselar la arista superior derecha. Lo primero es definir 2 conectores sobre la arista (en el mismo punto). Uno en la dirección de la arista (da igual el sentido) y el otro orgonal, apuntando hacia la bisectriz exterior:

//-- Dimensiones del cubo
size=[40,40,15];

//-- Conectores
//--      posicion                 direccion  cero
ec1 = [ [size[0]/2, 0, size[2]/2], [0,1,0],    0];
en1 = [ ec1[0],                    [1,0,1],    0];

Conviene visualizar los conectores para asegurarnos de que no nos hemos equivocado (Fig 1):

//-- Debug!
connector(ec1);
connector(en1);

y dibujar el cubo en transparente:

color("Yellow",0.4) cube(size,center=true);

Ahora llega el momento de la magia. Con el módulo bevel() se colocará una pieza cóncava sobre la arista (Fig 2)

bevel(ec1, en1, cr = 8, cres=10, l=size[1]+2);

Lo único que hay que hacer ahora es la diferencia, obteniéndose la arista biselada (Fig 3):

difference() { 
  cube(size,center=true);
  bevel(ec1, en1, cr = 8, cres=10, l=size[1]+2);
}

En general, en una pieza se harán más de un biselado. Primero se definen todos los connectores y luego se usa un bloque de este tipo:

difference() {
   my_part();
   bevel(a1,a2...); //-- Biselar la arista a
   bevel(b1,b2...); //-- Biserl a arista b
}

Como ejemplo, ver la (Fig 4).

Ejemplo 2

Fig. 5: Colocando los conectores para reforzar una pieza (click para ampliar)

Vamos a reforzar una pieza. El procedimiento es similar. Empezamos visualizando la pieza y creando los conectores (visualizándolos para depurar) (Fig 5); En este caso el conector normal al eje de unión tiene que estar apuntando hacia la bisectriz interna

size=[30,30,30];
th = 3; 

//-- Conectores
ec1 = [ [0,-size[1]/2+th,-size[2]/2+th], [1,0,0],  0];
en1 = [ ec1[0],                          [0,1,1], 0]; 

//-- Ver los conectores para depurar
connector(ec1);
connector(en1); 

//-- Dibujar la pieza a reforzar
difference() {
 cube(size,center=true);
 translate([0,th,th])
   cube([size[0]+2,size[1],size[2]],center=true);
}

Ahora añadimos el refuerzo con este comando:

bconcave_corner_attach(ec1,en1,l=th,cr=8,cres=0);

Fig. 6: Pieza con refuerzo

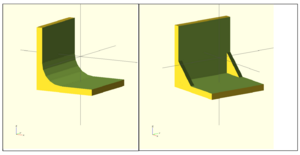
Jugando con los parámetros (radio, resolución...) y añadiendo más conectores se obtienen diferentes tipos de refuerzos:

Fig. 7: Distintos refuerzos

API

• bconcave_corner(cr=1,cres=4,th=1,l=10,ext_corner=false) : Obtener un esquina cóncava.
• bconcave_corner_attach (ec1,en1,l=th,cr=8,cres=0): Colocar una esquina cóncava como refuerzo
• bevel (ec1, en1, cr = 8, cres=10, l=size[1]+2): Colocar una pieza cóncaba para hacer el biselado de aristas exteriores

Repositorio

• Acceso al repositorio: https://github.com/Obijuan/obiscad

Autor

• Juan González Gómez (Obijuan)

Noticias

• 7/Sep/2012: Comenzada esta página