Diferencia entre revisiones de «Cinemática de brazos robóticos simples con Octave/Matlab»

De WikiRobotics
Saltar a: navegación, buscar
(→‎Ejemplo en Octave)
 
(No se muestran 86 ediciones intermedias del mismo usuario)
Línea 1: Línea 1:
 +
[[Archivo:Robot3-kinematics.png|thumb|right|300px| Cinemática de un brazo robot de 3 grados de libertad (''click para ampliar'')]]
 
== Introducción ==
 
== Introducción ==
 +
Se muestran ejemplos de cómo resolver la '''cinemática directa''' de tres brazos robóticos sencillos, de 1, 2 y 3 grados de libertad usando '''transformadas homogéneas''' y la herramienta [http://www.gnu.org/software/octave/ Octave] , corriendo en una máquina con Ubuntu Linux (11.10)
 +
 +
Los ejemplos se hicieron originalmente para los estudiantes de la asignatura de '''Control y Programación de Robots''', Ingeniería Industrial, Universidad Carlos III de Madrid (UC3M)
 +
 +
== Instalación ==
 +
 +
Instalación de octave en Ubuntu 11.10:
 +
 +
  sudo apt-get install octave3.2
 +
 +
Descargar el paquete [http://www.iearobotics.com/downloads/2010-10-12-ArmRobotKinematics/ArmRobotKinematics-v1.2.zip ArmRobotKinematics-v1.2.zip] con los ejemplos y descomprimirlo
 +
 +
== Robot 1 ==
 +
El primer ejemplo es un '''robot con un grado de libertad''' (<math>q_1</math>). Sólo es necesario usar una transformación homogénea determinada por una rotación de <math>q_1</math> grados alrededor del eje <math>x_1</math> y una traslación de <math>l_1</math> sobre el eje <math>y_1</math>:
 +
 +
<math>A_1=Rotx(q_1)Trasy(l_1)</math> donde:
 +
 +
<math>Rotx(a)=\left(\begin{array}{cccc}
 +
1 & 0 & 0 & 0\\
 +
0 & cos(a) & -sin(a) & 0\\
 +
0 & sin(a) & cos(a) & 0\\
 +
0 & 0 & 0 & 1\end{array}\right)</math>, <math>Trasy(l_1)=\left(\begin{array}{cccc}
 +
1 & 0 & 0 & 0\\
 +
0 & 1 & 0 & l_1\\
 +
0 & 0 & 1 & 0\\
 +
0 & 0 & 0 & 1\end{array}\right)
 +
</math>
 +
 +
 +
{| {{tablabonita}}
 +
| [[Archivo:Robot1-kinematics.png|thumb|300px|'''Fig 1''': Cinemática del robot 1 (''click para ampliar'')]]
 +
| [[Archivo:Robot1-pantallazo.png|thumb|300px|'''Fig 2''': Captura de pantalla de la ejecución de Robot1 en Octave(''click para ampliar'') ]]
 +
|}
 +
 +
En la '''Figura 1''' se muestra la geometría del robot y la nomenclatura empleada para los sistemas de referencia. En la '''figura 2''' se puede ver un pantallazo de la ejecución del programa para Octave.
 +
 +
=== Ejemplo ===
 +
 +
Arrancar octave y ejecutar el siguiente comando
 +
 +
octave:1> robot1(45)
 +
 +
Se le pasa como parámetro el ángulo <math>q_1</math> en grados. El programa calcula los puntos del robot y los dibuja en pantalla.
 +
 +
== Robot 2 ==
 +
Este segundo ejemplo es un brazo robot de '''2 grados de libertad''' (<math>q_1</math> y <math>q_2</math>). Las dos matrices de transformación son:
 +
 +
* <math>A_1=Rotx(q_1)Trasy(l_1)</math>
 +
* <math>A_2=Rotx(q_2)Trasy(l_2)</math>
 +
 +
donde: Rotx y Trasy son las mismas matrices del ejemplo 1
 +
 +
{| {{tablabonita}}
 +
| [[Archivo:Robot2-kinematics.png|thumb|300px|'''Fig 3''': Cinemática del robot 2 (''click para ampliar'')]]
 +
| [[Archivo:Robot2-pantallazo.png|thumb|300px|'''Fig 4''': Captura de pantalla de la ejecución de Robot2 en Octave(''click para ampliar'') ]]
 +
|}
 +
 +
En la '''Figura 3''' se muestra la geometría del robot y la nomenclatura empleada para los sistemas de referencia. En la '''figura 4''' se puede ver un pantallazo de la ejecución del programa para Octave.
 +
 +
=== Ejemplo ===
 +
 +
Arrancar octave y ejecutar el siguiente comando
 +
 +
octave:1> robot2(45,-55)
 +
 +
Se le pasa como parámetros los ángulos <math>q_1</math> y <math>q_2</math> en grados. El programa calcula los puntos del robot y los dibuja en pantalla.
 +
 +
== Robot 2 + 1 ==
 +
Robot con '''2 grados de libertad para posicionamiento''' del manipulador y '''1 para su orientación'''. La nueva matriz de transformación es:
 +
 +
* <math>A_3=Rotx(q_3)</math>
 +
 +
{| {{tablabonita}}
 +
| [[Archivo:Robot2 1-kinematics.png|thumb|300px|'''Fig 4''': Cinemática del robot 2+1 (''click para ampliar'')]]
 +
| [[Archivo:Robot2 1-pantallazo.png|thumb|300px|'''Fig 5''': Captura de pantalla de la ejecución de Robot2+1 en Octave(''click para ampliar'') ]]
 +
|}
 +
 +
En la '''Figura 4''' se muestra la geometría del robot y la nomenclatura empleada para los sistemas de referencia. En la '''figura 5''' se puede ver un pantallazo de la ejecución del programa para Octave.
 +
 +
=== Ejemplo ===
 +
 +
Arrancar octave y ejecutar el siguiente comando
 +
 +
octave:1> robot2_1(45,-55,60);
 +
 +
Se le pasa como parámetros los ángulos <math>q_1</math>, <math>q_2</math> y <math>q_2</math> en grados. El programa calcula los puntos del robot y los dibuja en pantalla.
  
 
== Robot 3 ==
 
== Robot 3 ==
 +
 +
Este ejemplo es un '''brazo robot de 3 grados de libertad''' (<math>q_0</math>, <math>q_1</math> y <math>q_2</math>). Las matrices de transformación homogéneas son:
 +
 +
* <math>A_0=Rotz(g_0)</math>
 +
* <math>A_1=Rotx(q_1)Trasy(l_1)</math>
 +
* <math>A_2=Rotx(q_2)Trasy(l_2)</math>
 +
 +
donde las matrices Rotx y Trasy son las mismas de los ejemplos 1 y 2, y Rotz es:
 +
 +
<math>Rotz(a)=\left(\begin{array}{cccc}
 +
cos(a) & -sin(a) & 0 & 0\\
 +
sin(a) & cos(a) & 0 & 0\\
 +
0 & 0 & 1 & 0\\
 +
0 & 0 & 0 & 1\end{array}\right)</math>
 +
 +
{| {{tablabonita}}
 +
| [[Archivo:Robot3-kinematics.png|thumb|300px|'''Fig 6''': Cinemática del Robot 3 (''click para ampliar'')]]
 +
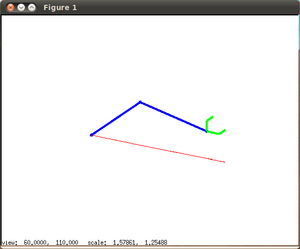
| [[Archivo:Robot3-captura1.png|thumb|300px|'''Fig 7''': Captura de pantalla de la ejecución de Robot3 en Octave (''Click para ampliar'')]]
 +
|}
 +
 +
En la '''Figura 6''' se muestra la geometría del robot y la nomenclatura empleada para los sistemas de referencia. En la '''figura 7''' se puede ver un pantallazo de la ejecución del programa para Octave.
 +
 +
=== Ejemplo ===
 +
 +
Arrancar octave y ejecutar el siguiente comando
 +
 +
octave:1> robot3(-10,45,-60)
 +
 +
Se le pasa como parámetros los ángulos <math>q_0</math>, <math>q_1</math> y <math>q_2</math> en grados. El programa calcula los puntos del robot y los dibuja en pantalla.
 +
 +
== Robot 3+1 ==
 +
Robot de '''4 grados de libertad''', 3 para posicionamiento del manipulador y 1 para su orientación.
 +
Las matrices de transformación homogéneas son:
 +
 +
* <math>A_0=Rotz(q_0)</math>
 +
* <math>A_1=Rotx(q_1)Trasy(l_1)</math>
 +
* <math>A_2=Rotx(q_2)Trasy(l_2)</math>
 +
* <math>A_3=Rotx(q_3)</math>
 +
 +
{| {{tablabonita}}
 +
| [[Archivo:Robot3 1-kinematics.png|thumb|300px|'''Fig 8''': Cinemática del Robot 3+1 (''click para ampliar'')]]
 +
| [[Archivo:Robot3 1-pantallazo.png|thumb|300px|'''Fig 9''': Captura de pantalla de la ejecución de Robot3+1 en Octave (''Click para ampliar'')]]
 +
|}
 +
 +
En la '''Figura 8''' se muestra la geometría del robot y la nomenclatura empleada para los sistemas de referencia. En la '''figura 9''' se puede ver un pantallazo de la ejecución del programa para Octave.
 +
 +
=== Ejemplo ===
 +
 +
Arrancar octave y ejecutar el siguiente comando
 +
 +
octave:1> robot3_1(-10,45,-60,60);
 +
 +
Se le pasa como parámetros los ángulos <math>q_0</math>, <math>q_1</math>, <math>q_2</math> y <math>q_3</math> en grados. El programa calcula los puntos del robot y los dibuja en pantalla.
 +
 +
== Descargas ==
  
 
{| {{tablabonita}}
 
{| {{tablabonita}}
−
| [[]]
+
| [http://www.iearobotics.com/downloads/2010-10-12-ArmRobotKinematics/ArmRobotKinematics-v1.2.zip ArmRobotKinematics-v1.2.zip]
 +
| Ejemplos para octave/Matlab. Versión 1.2
 +
|------------
 +
| [http://www.iearobotics.com/downloads/2010-10-12-ArmRobotKinematics/ArmRobotKinematics-1.1.zip ArmRobotKinematics-1.1.zip]
 +
| Ejemplos para octave. Versión 1.1
 +
|------------
 +
| [http://www.iearobotics.com/downloads/2010-10-12-ArmRobotKinematics/ArmRobotKinematics-1.0.zip ArmRobotKinematics-1.0.zip]
 +
| Ejemplos para Octave. Versión 1.0 ('''Obsoleta''')
 
|}
 
|}
  
 +
== Autor ==
 +
[[Juan Gonzalez:Main|Juan González Gómez]]
 +
 +
== Licencia ==
 +
{|{{tablabonita}}
 +
| [[Imagen:Cc logo.png]] This work is licensed under a [http://creativecommons.org/licenses/by-sa/3.0/es/ Creative Commons Attribution-ShareAlike 3.0 Spain License].
 +
|--------
 +
| [[Imagen:GPLv3-logo-red.png|left|150px]] El código está liberado bajo licencia GPLv3
 +
|}
  
 
== Repositorio SVN ==
 
== Repositorio SVN ==
  
 
* [http://svn.iearobotics.com/ArmRobotKinematics http://svn.iearobotics.com/ArmRobotKinematics]
 
* [http://svn.iearobotics.com/ArmRobotKinematics http://svn.iearobotics.com/ArmRobotKinematics]
 +
 +
== Enlaces ==
 +
* [[Cuadernos Técnicos|Índice de cuadernos técnicos]]
  
 
== Noticias ==
 
== Noticias ==
 +
* '''28/Abril/2012''':
 +
** Version 1.2 liberada: Modificados los ejemplos para funcionar en Matlab (además de octave)
 +
* '''20/Octubre/2010''':
 +
** Añadidos los ejemplos Robot2+1 y Robot3+1
 +
** Versión 1.1 liberada
 +
* '''12/Octubre/2010''':
 +
** Primera versión de esta página
 +
** Versión 1.0 liberada
 
* '''07/Octubre/2010''': Comenzada esta página
 
* '''07/Octubre/2010''': Comenzada esta página

Revisión actual del 07:25 28 abr 2012

Cinemática de un brazo robot de 3 grados de libertad (click para ampliar)

Introducción

Se muestran ejemplos de cómo resolver la cinemática directa de tres brazos robóticos sencillos, de 1, 2 y 3 grados de libertad usando transformadas homogéneas y la herramienta Octave , corriendo en una máquina con Ubuntu Linux (11.10)

Los ejemplos se hicieron originalmente para los estudiantes de la asignatura de Control y Programación de Robots, Ingeniería Industrial, Universidad Carlos III de Madrid (UC3M)

Instalación

Instalación de octave en Ubuntu 11.10: 

 sudo apt-get install octave3.2

Descargar el paquete ArmRobotKinematics-v1.2.zip con los ejemplos y descomprimirlo

Robot 1

El primer ejemplo es un robot con un grado de libertad (<math>q_1</math>). Sólo es necesario usar una transformación homogénea determinada por una rotación de <math>q_1</math> grados alrededor del eje <math>x_1</math> y una traslación de <math>l_1</math> sobre el eje <math>y_1</math>:

<math>A_1=Rotx(q_1)Trasy(l_1)</math> donde:

<math>Rotx(a)=\left(\begin{array}{cccc} 1 & 0 & 0 & 0\\ 0 & cos(a) & -sin(a) & 0\\ 0 & sin(a) & cos(a) & 0\\ 0 & 0 & 0 & 1\end{array}\right)</math>, <math>Trasy(l_1)=\left(\begin{array}{cccc} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & l_1\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1\end{array}\right) </math>


Fig 1: Cinemática del robot 1 (click para ampliar)
Fig 2: Captura de pantalla de la ejecución de Robot1 en Octave(click para ampliar)

En la Figura 1 se muestra la geometría del robot y la nomenclatura empleada para los sistemas de referencia. En la figura 2 se puede ver un pantallazo de la ejecución del programa para Octave.

Ejemplo

Arrancar octave y ejecutar el siguiente comando 

octave:1> robot1(45)

Se le pasa como parámetro el ángulo <math>q_1</math> en grados. El programa calcula los puntos del robot y los dibuja en pantalla.

Robot 2

Este segundo ejemplo es un brazo robot de 2 grados de libertad (<math>q_1</math> y <math>q_2</math>). Las dos matrices de transformación son:

  • <math>A_1=Rotx(q_1)Trasy(l_1)</math>
  • <math>A_2=Rotx(q_2)Trasy(l_2)</math>

donde: Rotx y Trasy son las mismas matrices del ejemplo 1

Fig 3: Cinemática del robot 2 (click para ampliar)
Fig 4: Captura de pantalla de la ejecución de Robot2 en Octave(click para ampliar)

En la Figura 3 se muestra la geometría del robot y la nomenclatura empleada para los sistemas de referencia. En la figura 4 se puede ver un pantallazo de la ejecución del programa para Octave.

Ejemplo

Arrancar octave y ejecutar el siguiente comando 

octave:1> robot2(45,-55)

Se le pasa como parámetros los ángulos <math>q_1</math> y <math>q_2</math> en grados. El programa calcula los puntos del robot y los dibuja en pantalla.

Robot 2 + 1

Robot con 2 grados de libertad para posicionamiento del manipulador y 1 para su orientación. La nueva matriz de transformación es:

  • <math>A_3=Rotx(q_3)</math>
Fig 4: Cinemática del robot 2+1 (click para ampliar)
Fig 5: Captura de pantalla de la ejecución de Robot2+1 en Octave(click para ampliar)

En la Figura 4 se muestra la geometría del robot y la nomenclatura empleada para los sistemas de referencia. En la figura 5 se puede ver un pantallazo de la ejecución del programa para Octave.

Ejemplo

Arrancar octave y ejecutar el siguiente comando 

octave:1> robot2_1(45,-55,60);

Se le pasa como parámetros los ángulos <math>q_1</math>, <math>q_2</math> y <math>q_2</math> en grados. El programa calcula los puntos del robot y los dibuja en pantalla.

Robot 3

Este ejemplo es un brazo robot de 3 grados de libertad (<math>q_0</math>, <math>q_1</math> y <math>q_2</math>). Las matrices de transformación homogéneas son:

  • <math>A_0=Rotz(g_0)</math>
  • <math>A_1=Rotx(q_1)Trasy(l_1)</math>
  • <math>A_2=Rotx(q_2)Trasy(l_2)</math>

donde las matrices Rotx y Trasy son las mismas de los ejemplos 1 y 2, y Rotz es:

<math>Rotz(a)=\left(\begin{array}{cccc} cos(a) & -sin(a) & 0 & 0\\ sin(a) & cos(a) & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1\end{array}\right)</math>

Fig 6: Cinemática del Robot 3 (click para ampliar)
Fig 7: Captura de pantalla de la ejecución de Robot3 en Octave (Click para ampliar)

En la Figura 6 se muestra la geometría del robot y la nomenclatura empleada para los sistemas de referencia. En la figura 7 se puede ver un pantallazo de la ejecución del programa para Octave.

Ejemplo

Arrancar octave y ejecutar el siguiente comando 

octave:1> robot3(-10,45,-60)

Se le pasa como parámetros los ángulos <math>q_0</math>, <math>q_1</math> y <math>q_2</math> en grados. El programa calcula los puntos del robot y los dibuja en pantalla.

Robot 3+1

Robot de 4 grados de libertad, 3 para posicionamiento del manipulador y 1 para su orientación. Las matrices de transformación homogéneas son:

  • <math>A_0=Rotz(q_0)</math>
  • <math>A_1=Rotx(q_1)Trasy(l_1)</math>
  • <math>A_2=Rotx(q_2)Trasy(l_2)</math>
  • <math>A_3=Rotx(q_3)</math>
Fig 8: Cinemática del Robot 3+1 (click para ampliar)
Fig 9: Captura de pantalla de la ejecución de Robot3+1 en Octave (Click para ampliar)

En la Figura 8 se muestra la geometría del robot y la nomenclatura empleada para los sistemas de referencia. En la figura 9 se puede ver un pantallazo de la ejecución del programa para Octave.

Ejemplo

Arrancar octave y ejecutar el siguiente comando 

octave:1> robot3_1(-10,45,-60,60);

Se le pasa como parámetros los ángulos <math>q_0</math>, <math>q_1</math>, <math>q_2</math> y <math>q_3</math> en grados. El programa calcula los puntos del robot y los dibuja en pantalla.

Descargas

ArmRobotKinematics-v1.2.zip Ejemplos para octave/Matlab. Versión 1.2
ArmRobotKinematics-1.1.zip Ejemplos para octave. Versión 1.1
ArmRobotKinematics-1.0.zip Ejemplos para Octave. Versión 1.0 (Obsoleta)

Autor

Juan González Gómez

Licencia

Cc logo.png This work is licensed under a Creative Commons Attribution-ShareAlike 3.0 Spain License.
150px El código está liberado bajo licencia GPLv3

Repositorio SVN

Enlaces

Noticias

  • 28/Abril/2012:
    • Version 1.2 liberada: Modificados los ejemplos para funcionar en Matlab (además de octave)
  • 20/Octubre/2010:
    • Añadidos los ejemplos Robot2+1 y Robot3+1
    • Versión 1.1 liberada
  • 12/Octubre/2010:
    • Primera versión de esta página
    • Versión 1.0 liberada
  • 07/Octubre/2010: Comenzada esta página
Obtenido de «http://iearobotics.com/wiki/index.php?title=Cinemática_de_brazos_robóticos_simples_con_Octave/Matlab&oldid=14096»