Diferencia entre revisiones de «Videoblog»

De WikiRobotics
Saltar a: navegación, buscar
(→‎9 Jugando con vectores en Freecad y Pyooml)
 
(No se muestran 45 ediciones intermedias del mismo usuario)
Línea 5: Línea 5:
 
== Introducción ==
 
== Introducción ==
 
En estos vídeos cortos mostraré cosas que me parecen interesantes: '''píldoras de conocimiento''', demostraciones, últimas novedades, noticias, etc.  Siempre la temática en común es '''Software libre''', '''hardware libre''' y '''patrimonio tecnológico de la humanidad'''. No estoy interesado en la tecnología que no es libre.
 
En estos vídeos cortos mostraré cosas que me parecen interesantes: '''píldoras de conocimiento''', demostraciones, últimas novedades, noticias, etc.  Siempre la temática en común es '''Software libre''', '''hardware libre''' y '''patrimonio tecnológico de la humanidad'''. No estoy interesado en la tecnología que no es libre.
 +
 +
{|  style="border: 1px solid darkgray; width:100%"
 +
|- style="background: #cedff2;"
 +
! A partir del capítulo 12, [https://github.com/Obijuan/videoblog/wiki la wiki se ha migrado a esta nueva en github]
 +
|}
 +
  
  
Línea 782: Línea 788:
 
|}
 
|}
  
−
== 9 Jugando con vectores en Freecad y Pyooml ==
+
== 9 Jugando con vectores en Freecad y Pyooml (Parte 1) ==
 
{|  style="border: 1px solid darkgray; width:100%"  
 
{|  style="border: 1px solid darkgray; width:100%"  
 
|- style="background: #cedff2;"
 
|- style="background: #cedff2;"
−
! [ '''Video blog 9''']
+
! [https://www.youtube.com/watch?v=AszB05pi9VI&index=9&list=PLmnz0JqIMEzVo7w2pv6Q04QgRaBTkqR30 '''Video blog 9''']
 
|}
 
|}
  
Línea 843: Línea 849:
 
| [[Archivo:Video-tut-9-exp-5.png|thumb|400px| Vector v2 visualizado (''click para ampliar'')]]
 
| [[Archivo:Video-tut-9-exp-5.png|thumb|400px| Vector v2 visualizado (''click para ampliar'')]]
 
|}
 
|}
 +
 +
Vamos a '''sumar los vectores''' y visualizar el resultado. Creamos el objeto sv3 que dibujará el vector suma:
 +
 +
>>> sv3 = svector(v1 + v2)
 +
 +
Cambiamos el '''color a amarillo''' para distinguirlo de v1 y v2:
 +
 +
>>> sv3.color("yellow")
 +
 +
Por defecto los vectores se dibujan en el origen. Vamos a trasladarlo al extremo de v1 para visualizar la '''ley del paralelogramo''':
 +
 +
>>> sv3.translate(v1)
  
 
{|
 
{|
−
| [[|thumb|400px|  (''click para ampliar'')]]
+
| [[Archivo:Video-tut-9-exp-6.png|thumb|400px| Visualizando el vector suma v1 + v2 (''click para ampliar'')]]
−
| [[|thumb|400px| (''click para ampliar'')]]
+
| [[Archivo:Video-tut-9-exp-7.png|thumb|400px| Ley del paralelogramo (''click para ampliar'')]]
 
|}
 
|}
 +
 +
También podemos calcular el producto vectorial de v1 y v2. Será un vector perpendicular al plano formado por v1 y v2. Para visualizarlo mejor, el resultado lo normalizamos y lo multiplicamos por 10 para que esa sea su módulo:
 +
 +
>>> v4 = v1.cross(v2).normalize() * 10
 +
 +
Ahora los mostramos en 3D, en color azul:
 +
 +
>>> sv4 = svector(v4).color("blue")
 +
 +
Comprobamos empíricamente que el producto vectorial NO es conmutativo. Si ahora multiplicamos v2 por v1, obtenemos el mismo vector, pero en sentido contrario:
 +
 +
>>> sv5 = svector( v2.cross(v1).normalize() * 10 )
  
 
{|
 
{|
−
| [[|thumb|400px|  (''click para ampliar'')]]
+
| [[Archivo:Video-tut-9-exp-8.png|thumb|400px| Visualizando el producto vectorial de v1 x v2 (''click para ampliar'')]]
−
| [[|thumb|400px|  (''click para ampliar'')]]
+
| [[Archivo:Video-tut-9-exp-9.png|thumb|400px| Visualizando el producto vectorial de v2 x v1 (''click para ampliar'')]]
 +
|}
 +
 
 +
Terminamos este ejemplo haciendo una diferencia entre el vector azul (v4) y el amarillo (v1 + v2):
 +
 
 +
>>> sv6 = svector ( v4 - (v1 + v2)).color("green")
 +
 
 +
y lo trasladamos al extremo del amarillo, para ver mejor la diferencia:
 +
 
 +
>>> sv6.translate(v1 + v2)
 +
 
 +
{|
 +
| [[Archivo:Video-tut-9-exp-10.png|thumb|400px| Visualizando la diferencia en verde: v4 - (v1  + v2) (''click para ampliar'')]]
 +
|}
 +
 
 +
== 10 Jugando con vectores en Freecad y Pyooml (Parte 2) ==
 +
{|  style="border: 1px solid darkgray; width:100%"
 +
|- style="background: #cedff2;"
 +
! [https://www.youtube.com/watch?v=BHZn0UeX18M&list=PLmnz0JqIMEzVo7w2pv6Q04QgRaBTkqR30&index=10 '''Video blog 10''']
 
|}
 
|}
  
 
{|
 
{|
−
| [[|thumb|400px|  (''click para ampliar'')]]
+
| [[Archivo:Videoblog-10-exp-0.png|500px|]]
−
| [[|thumb|400px|  (''click para ampliar'')]]
 
 
|}
 
|}
 +
 +
 +
=== Descripción ===
 +
Además de vectores, con pyooml también podemos poner '''puntos''' y '''sistemas de referencia'''. Mediante rotaciones y traslaciones los colocamos donde se necesiten
 +
 +
=== Explicación ===
 +
 +
Lazamos freecad desde el directorio donde está el proyecto friki. Abrimos la consola de python. Lo primero que hacemos es cargar las bibliotecas que vamos a usar:
 +
 +
>>> from FreeCAD import Vector
 +
>>> from pyooml import *
 +
 +
Los '''sistemas de referencia''' los visualizamos con la clase '''frame()''' de pyooml:
 +
 +
>>> frame()
 +
 +
Vamos a colocar un '''punto'''. Definimos el vector v, y colocamos un punto en esa posición mediante '''point()''':
 +
 +
>>> v = Vector(10,10,10)
 +
>>> p = point(v)
 +
 +
{|
 +
| [[Archivo:Video-tut-9-exp-11.png|thumb|400px| Sistema de referencia en el origen  (''click para ampliar'')]]
 +
| [[Archivo:Video-tut-9-exp-12.png|thumb|400px| Visualizando punto en la posición dada por el vector v (''click para ampliar'')]]
 +
|}
 +
 +
Mostramos el vector de posición del punto, mediante un vector amarillo:
 +
 +
>>> sv = svector(v).color("yellow")
 +
 +
Dibujamos un cubo con uno de los vértices en el punto, y lo hacemos '''transparente''' con el método '''ice()'''
 +
 +
>>> c = cube(v)
 +
>>> c.ice(80)
 +
 +
{|
 +
| [[Archivo:Video-tut-9-exp-13.png|thumb|400px| Vector de posición del punto  (''click para ampliar'')]]
 +
| [[Archivo:Video-tut-9-exp-14.png|thumb|400px| Cubo transparente, con uno de los vértices en el punto (''click para ampliar'')]]
 +
|}
 +
 +
Creamos otro sistema de referencia:
 +
 +
>>> f2 = frame()
 +
 +
y lo posicionamos en v:
 +
 +
>>> f2.translate(v)
 +
 +
Añadimos un tercer sistema de referencia y lo rotamos 30 grados con respecto a su eje x:
 +
 +
>>> f3 = frame()
 +
>>> f3.rotx(30)
 +
 +
{|
 +
| [[Archivo:Video-tut-9-exp-15.png|thumb|400px| Otros sistema de referencia, en la posición dada por v  (''click para ampliar'')]]
 +
| [[Archivo:Video-tut-9-exp-16.png|thumb|400px| Sistema de referencia f3, rotado con respecto al inicial (''click para ampliar'')]]
 +
|}
 +
 +
Lo situamos en la posición v:
 +
 +
>>> f3.translate(v)
 +
 +
y lo desplazamos 10mm en dirección del eje de las x:
 +
 +
>>> f3.translate(10,0,0)
 +
 +
Vemos lo fácil que es montar nuestros sistemas de referencia para definir la cinemática de nuestros diseños :-)
 +
 +
{|
 +
| [[Archivo:Video-tut-9-exp-17.png|thumb|400px| Sistema f3 desplazado a la posición v  (''click para ampliar'')]]
 +
| [[Archivo:Video-tut-9-exp-18.png|thumb|400px| Sistema f3 desplazado una distancia adicional en su eje x (''click para ampliar'')]]
 +
|}
 +
 +
==== Ejemplo 3 ====
 +
 +
En este ejemplo se mostrará un dibujo del '''campo vectorial magnético''' a una distancia r provocado por una corriente que circula por un cable. Lo primero es ir a file/open y abrir el script: '''example-vector-field.py'''.  En vez de ejecutarlo de manera interactiva, como antes, lo vamos a ejecutar de golpe. Le damos al triángulo verde superior. Se nos crea una ventana nueva y al cabo de unos segundos nos aparece el campo vectorial, junto con cable y un vector azul grande que indica el sentido de desplazamiento de la corriente.
 +
 +
{|
 +
| [[Archivo:Video-tut-9-exp-19.png|thumb|400px| Ejemplo de un campo vectorial. Imagen + código  (''click para ampliar'')]]
 +
| [[Archivo:Video-tut-9-exp-20.png|thumb|400px| Ejemplo del campo vectorial (''click para ampliar'')]]
 +
|}
 +
 +
== 11 Cinemática directa de un brazo robot de 2 grados de libertad con Freecad y Pyooml ==
 +
{|  style="border: 1px solid darkgray; width:100%"
 +
|- style="background: #cedff2;"
 +
! [https://www.youtube.com/watch?v=2kPvyDbLMts&list=PLmnz0JqIMEzVo7w2pv6Q04QgRaBTkqR30&index=11 '''Video blog 11''']
 +
|}
 +
 +
{|
 +
| [[Archivo:Videoblog-11-exp-0.png|500px|]]
 +
|}
 +
 +
 +
=== Descripción ===
 +
Ejemplo de lo fácil que es definir la cinemática directa de un brazo robot con 2 grados de libertad usando Freecad y Pyooml
 +
 +
=== Explicación ===
 +
El '''brazo robot''' de ejemplo que usaremos es el de la '''figura 1'''. Consta de 2 articulaciones de ángulos '''a1''' y '''a2''', unidas mediante dos eslabones de longitudes '''L1''' y '''L2'''. En total hay 3 sistemas de referencia: uno en el mundo, y uno en cada extremo de los eslabones.
 +
 +
Arrancamos freecad desde el directorio donde tenemos el [https://github.com/Obijuan/friki proyecto friki] y abrimos la '''consola de python''' para trabajar de forma interactiva
 +
 +
{|
 +
| [[Archivo:Videoblog-11-exp-1.png|thumb|400px| '''Fig. 1''': Cinemática del robot de 2 grados de libertad (''click para ampliar'')]]
 +
| [[Archivo:Videoblog-11-exp-2.png|thumb|400px| Freecad con la consola de python abierta, listo para diseñar la cinemática del robot  (''click para ampliar'')]]
 +
|}
 +
 +
Importamos las '''bibliotecas''' que vamos a usar, como siempre:
 +
 +
>>> from FreeCAD import Vector
 +
>>> from pyooml import *
 +
 +
Definimos los '''parámetros de nuestro robot''': los ángulos y las longitudes de los eslabones:
 +
 +
  >>> a1 = -60
 +
  >>> a2 = 70
 +
  >>> L1 = 40
 +
  >>> L2 = 40
 +
 +
Ahora los '''vectores de los eslabones''':
 +
 +
>>> v1 = Vector(L1, 0, 0)
 +
>>> v2 = Vector(L2, 0, 0)
 +
 +
y los '''elementos gráficos''': 3 sistemas de referencia y 2 vectores sólidos para los eslabones:
 +
 +
  >>> f0 = frame()
 +
  >>> f1 = frame()
 +
  >>> f2 = frame()
 +
  >>> sv1 = svector(v1).color("yellow")
 +
  >>> sv2 = svector(v2).color("yellow")
 +
 +
Por último '''definimos las transformaciones''', referidas al sistema de referencia móvil:
 +
 +
  >>> import HMatrix
 +
  >>> Ma = HMatrix.Roty(a1)
 +
  >>> Mb = HMatrix.Translation(v1)
 +
  >>> Mc = HMatrix.Roty(a2)
 +
  >>> Md = HMatrix.Translation(v2)
 +
 +
Empezamos a aplicar las transformaciones a todos los elementos. Primero el '''vector del eslabón 1''':
 +
 +
  >>> sv1.T = Ma
 +
 +
Le aplicamos la '''transformación Ma''' (que es una rotación alrededor del eje y un ángulo a1)
 +
 +
{|
 +
| [[Archivo:Videoblog-11-exp-3.png|thumb|400px| Elementos gráficos creados (superpuestos) (''click para ampliar'')]]
 +
| [[Archivo:Videoblog-11-exp-4.png|thumb|400px| Aplicada transformación Ma sobre vector sv1 (''click para ampliar'')]]
 +
|}
 +
 +
Colocamos el '''sistema de referencia f1''' al final del eslabón 1, aplicando primero la transformación Ma y luego la Mb. Esto se consigue mediante la '''multiplicación de las matrices'''. Estas transformación siempre están referidas al sistema móvil
 +
 +
>>> f1.T = Ma * Mb
 +
 +
Colocamos el '''vector del eslabón 2'''. Aplicamos las transformaciones anteriores más la corresponidente a la rotación de la articulación a2:
 +
 +
>>> sv2.T = Ma * Mb * Mc
 +
 +
{|
 +
| [[Archivo:Videoblog-11-exp-5.png|thumb|400px| Aplicada transformación Ma * Mb sobre el sistema f1 (''click para ampliar'')]]
 +
| [[Archivo:Videoblog-11-exp-6.png|thumb|400px| Aplicada tansformación Ma * Mb * Mc sobre sv2 (''click para ampliar'')]]
 +
|}
 +
 +
y el '''sistema de referencia f2''' sobre el '''extremo del eslabón 2''':
 +
 +
>>> f2.T = Ma * Mb * Mc * Md
 +
 +
La '''posición del extremo final''' la obtenemos muy fácilmente multiplicando esta última matriz de transformación por el vector de su origen (0,0,0). Nos devuelve las coordenadas con respecto al sistema del mundo f0. Con esto hemos resuelto la cinemática directa del robot: conocemos en todo momento la posición del extremo final en función de los ángulos a1, a2 y la geometría del robot (l1, l2):
 +
 +
>>> vr = f2.T.multiply(Vector(0,0,0))
 +
>>> svr = svector(vr).color("orange")
 +
 +
{|
 +
| [[Archivo:Videoblog-11-exp-7.png|thumb|400px| Aplicada transformación Ma * Mb  * Mc * Md sobre f2 (''click para ampliar'')]]
 +
| [[Archivo:Videoblog-11-exp-8.png|thumb|400px| Cinemática directa resuelta: Vector de posición del extremo (''click para ampliar'')]]
 +
|}
 +
 +
Vamos a colocar los '''eslabones del robot''', para que quede más bonito. Primero los creamos. Los hacemos transparentes para poder ver la cinemática:
 +
 +
>>> l1 = link(l = L1, D = 10, w = 5).ice(80)
 +
>>> l2 = link(l = L2, D = 10, w = 3).ice(80)
 +
 +
Primero es elabón 2. Lo colocamos aplicando la transformación Ma * Mb * Mc
 +
 +
>>> l2.T = Ma * Mb * Mc
 +
 +
{|
 +
| [[Archivo:Videoblog-11-exp-9.png|thumb|400px| Eslabones creados. Están superpuestos, y situados en el origen (''click para ampliar'')]]
 +
| [[Archivo:Videoblog-11-exp-10.png|thumb|400px| Eslabón 2 colocado en su sitio. Definido por la transformación: Ma * Mb * Mc (''click para ampliar'')]]
 +
|}
 +
 +
Ahora el eslabón 1. Aplicamos la transformación Ma:
 +
 +
>>> l1.T = Ma
 +
 +
Para terminar ponemos una base al robot:
 +
 +
>>> base = sphere(r = 14, angle1 = 0).translate(0, 0, -6).ice(80)
 +
 +
{|
 +
| [[Archivo:Videoblog-11-exp-11.png|thumb|400px| Eslabón 1 colocado (''click para ampliar'')]]
 +
| [[Archivo:Videoblog-11-exp-12.png|thumb|400px| Robot final, con su base (''click para ampliar'')]]
 +
|}
 +
 +
=== Ejercicio ===
 +
 +
Se deja como ejercicio añadir un grado de libertad más en el robot, de manera que el robot completo pueda girar en torno al '''eje z''' del sistema de referencia del mundo. La matriz homogenea para hacer esta tansformación es '''HMatrix.Rotz(angle)'''.
 +
 +
{|
 +
| [[Archivo:Videoblog-11-exp-13.png|thumb|400px| Robot de 3 Grados de libertad (''click para ampliar'')]]
 +
|}
 +
 +
== 12 Proyecto Icestorm: Herramientas libres para sintetizar diseños en FPGAs ==
 +
{|  style="border: 1px solid darkgray; width:100%"
 +
|- style="background: #cedff2;"
 +
! [https://www.youtube.com/watch?v=XoQUm0jBdfs '''Video blog 12''']
 +
|}
 +
 +
A partir del capítulo 12, [https://github.com/Obijuan/videoblog/wiki la wiki se ha migrado a esta nueva en github]
  
 
== Repositorio ==
 
== Repositorio ==
Línea 894: Línea 1160:
  
 
== Noticias ==
 
== Noticias ==
 +
* '''24/Dic/2015''': Episodio 12: Migrado a la [https://github.com/Obijuan/videoblog/wiki nueva wiki en github]
 +
* '''15/Abril/2015''': Episodio 11
 +
* '''12/Abril/2015''':
 +
** Episodio 10
 +
** Episodio 9
 
* '''03/Abril/2015''': Episodio 8
 
* '''03/Abril/2015''': Episodio 8
 
* '''02/Abril/2015''': Episodio 7
 
* '''02/Abril/2015''': Episodio 7

Revisión actual del 02:57 23 ene 2016

Píldoras de conocimiento

Contenido

Introducción

En estos vídeos cortos mostraré cosas que me parecen interesantes: píldoras de conocimiento, demostraciones, últimas novedades, noticias, etc. Siempre la temática en común es Software libre, hardware libre y patrimonio tecnológico de la humanidad. No estoy interesado en la tecnología que no es libre.

A partir del capítulo 12, la wiki se ha migrado a esta nueva en github


Claves

Tutorial. Tutoriales. Videotutorial. Videotutoriales. Videoblog. Patrimonio tecnológico de la humanidad. Píldoras de conocimiento

Descargas

Todos los ejemplos están en el repositorio de este videoblog en github

PLAYLIST

PLAYLIST DEL VIDEOBLOG

1 Demo: Moviendo servos con Widgets interactivos desde un notebook de Jupyter

Video blog 1
(click para ampliar)
(click para ampliar)

Descripción

Demostración del movimiento de un servo a través de un notebook usando los nuevos widgets interactivos de IPython 3.0 (Proyecto Jupyter). La nueva versión de IPython la puedes instalar siguiendo estas instrucciones

El concepto de notebook es muy potente e interesante. Está pensado fundamentalmente para que los usen científicos e ingenieros, pudiendo representar ecuaciones, programar algoritmos, escribir documentación, poner vídeos... todo en una página abierta desde el navegador.

Pero como los notebooks se programa en python, que es un lenguaje de propósito general, se pueden adaptar fácilmente para diferentes aplicaciones. Una de ellas es controlar servos. Esto abre las puertas para poder controlar robots artículados basados en servos. Y así se pueden probar algoritmos nuevos de generación de locomoción, caminatas, etc. También es muy útil para depurar la mecánica de los robots y ajustar las posiciones iniciales de los servos. Todo ello desde el navegador. Multiplaforma. Sencillo. Y por supuesto libre.

Los ejemplos están subidos en este repositorio de github

Juan Luis Cano. Segunda edición del curso python para científicos e ingenieros (click para ampliar)

La inspiración de esta aplicación ha venido por los excelentos tutoriales que ha dado Juan Luis Cano, de Pybonnacci, en la segunda edición del curso python para científicos e ingenieros organizado por la Universidad de Alicante. Con ellos he descubierto los widgets interactivos y lo fáciles que son de usar en el nuevo Ipython 3.0. ¡Gracias Juanlu!  :-)

Hardware usado en la demo

  • Un servo Futaba 3003, instalado en un módulo Y1 (para apreciar mejor el movimiento)
  • La placa bq ZUM BT-328, donde se conecta el servo. También se puede usar una placa Arduino. Se conecta al portátil a través de un cable USB

Agradecimientos

  • A Juan Luis Cano, de Pybonacci, por el excelente curso de python. ¡Muchísimas gracias!

Enlaces

2 Moviendo un servo desde un Notebook de Ipython (parte 2)

Video blog 2
(click para ampliar)

Descripción

Explicación rápida de los pasos a seguir para mover los servos desde nuestros notebooks de Ipython 3.0

Explicación

Los pasos a seguir son los siguientes:

Paso 1: Instalar Ipython 3.0

Esto depende del SO y entorno python que tengáis. Podéis encontrar instrucciones en este enlace

En mi portátil tengo Ubuntu 14.10. Las pruebas las he hecho instalando Anaconda y luego ejecutando: 

conda update conda
conda update ipython ipython-notebook ipython-qtconsole

Una vez instalador podemos hacer una comprobación rápida, ejecutando en el terminal esto: 

$ ipython --version
3.0.0


Paso 2: Instalar pyserial

La instalación de la biblioteca pyserial dependen también de vuesltro entorno. Aquí os dejo un enlace a las instrucciones

Desde ubuntu se instala muy fácilmente con el siguiente comando: 

sudo apt-get install python-serial

Podemos comprobar si lo tenéis correctamente instalado ejecutando el intérprete de ipython e importando la biblioteca con import serial. Si no estuviese correctamente instalada aparecería un mensaje de error

Comprobando si la biblioteca pyserial está instalada (click para ampliar)

Pase 3: Bajarse el proyecto zum-servos de github

El firmware, los programas en python y los notebooks están en el proyecto zum-servos en github. Bien descargar el zip o clonar el proyecto en tu ordenador local.

Paso 5: Realizar las conexiones en la plaza zum / Arduino

  • Conectar el servo Futaba 3003 o compatible al PIN #9 de la placa zum / arduino
  • Conectar la plaza zum / arduino al ordenador, mediante el cable USB
Conexión del servo a la placa zum

Paso 6: Cargar el firmware zum_servos_fw.ino a la placa zum / Arduino

Arrancar el entorno del arduino. Abrir el firmware de la carpeta zum-servos/firmware/zum_servo_fw. Seleccionar la placa, el puerto y cargar el firmware en la placa zum / arduino. Para descargar en la zum hay que seleccionar la placa: Arduino BT w/ ATmega328

El firmware para mover servos cargado en el entorno de arduino (click para ampliar)

Paso 7: Lanzar el notebook de zum-servos-example-1

Vamos a la carpeta zum-servos/python y arrancamos el notebook: 

$ ipython notebook

En una pestaña del navegador nos aparecerá la página principal del Ipython Notebook con todos los notebooks que podemos seleccionar. Pinchamos en zum-servos-example-1.ipynb para que se nos abra el notebook

Ipython 3.0 notebook lanzado (click para ampliar)
Abierto el notebook zum-servos-example-1 (click para ampliar)

Paso 8: Ejecutar el notebook

Bajamos hasta la zona donde comienza el código en python y ejecutamos las celdas. Antes de ejecutar la celda 4, configurar el nombre del puerto serie en el que está conectada la placa zum / arduino. En mi portátil está en el puerto serie /dev/ttyUSB0

Parte donde comienza el código en python (click para ampliar)
Configurar el puerto serie (click para ampliar)

Por último ejecutamos la celda 12 y nos aparece la barra deslizadora. Al desplazarla se moverá el servo. La última celda es un ejemplo de generacion de una secuencia de movimientos del servo.

El widget interactivo para mover el servo y el código para la generación de la secuencia de movimiento (click para ampliar)

3 El nuevo Openscad 2015.03

Video blog 3
(click para ampliar)

Descripción

En Marzo de 2015 se acaba de liberar la nueva versión de Openscad: 2015.03. Se describen brevemente las principales mejoras: texto integrado, listas por comprensión, comando offset, comando surface y mejora de la interfaz gráfica

Explicación

Al arrancar el openscad 2015.03 aparece una pantalla de bienvenida que nos permite rápidamente crear un diseño nuevo, cargar alguno reciente o acceder a los ejemplos y documentación. Vamos a crear un documento nuevo pinchando en new.

Lo primero que vemos es la mejora en la interfaz gráfica. Se han añadido botones en el visor para cambiar las vistas y las propiedades de visualización. Muy cómodo. Especialmente útil es el botón de centrado de la pieza.

Pantalla de bienvenida en openscad 2015.03 (click para ampliar)
Openscad 2015.03 recién arrancado (click para ampliar)

Creamos un cubo "hola mundo" para trastear un poco con el nuevo openscad

Cubo "hola mundo" de prueba (click para ampliar)

Una de las mejoras es la creación de texto en 3D. Antes había que utilizar bibliotecas externas. Ahora está integrado en Openscad. Esto hace muy fácil el crear llaveros y objetos con texto 3D. Se realiza con el comando text. Este es un ejemplo "hola mundo" que genera el texto "¡Hola!" en 3D 

linear_extrude(height = 5)
text("¡Hola!", size = 50, halign = "center", font = "Liberation Sans", $fn = 20);

Para acceder a los tipos de letras que ha detectado openscad en nuestro sistema, nos vamos a la opción Help / Font List y se nos despliega una ventana con todos los tipos que podemos usar.

Creación de texto en 3D (click para ampliar)
Selección de las fuentes para el texto (click para ampliar)

Otra novedad: Las listas por comprensión. Es un método muy potente para crear listas de elementos. Permite por ejemplo crear polígonos y figuras 2D a partir de sus vértices: 

l = [for (i=[0:4], a = 360 * i/5) [10 * sin(a), 10*cos (a)]];
echo(l);    
polygon(l);
Creando un pentagono mediante una lista por comprensión (click para ampliar)

Otro comando nuevo introducido es offset, que nos permite agrandar o achicar figuras 2D una distancia fija. Muy útil para hacer piezas que encajen unas dentro de otras, definiendo una tolerancia.

Este es un ejemplo sencillo de uso de offset: 


offset(1)
union() {
  square([10, 20]);
  square([20, 10]);
}
Figura 2D sin aplicar offset (original) (click para ampliar)
Offset positivo de 1mm (click para ampliar)
offset negativo de 1mm (click para ampliar)

El comendo surface permite crear un objeto 3D a partir de una imagen. Según el color de los pixeles de la imagen se crean las partes del objeto a diferentes alturas. Este es un ejemplo usando el logo de obijuan academy: 

surface("logo.png", center = true);


Logo de obijuan academy usado para generar un objeto 3D con surface (click para ampliar)
Pieza creada con el comando surface (click para ampliar)

Descarga de ficheros

text-example.scad Ejemplo de creación de letras 3D: "¡Hola!"
list.scad Ejemplo de uso de las listas por comprensión
offset.scad Ejemplo del comando offset
surface_image.scad Ejemplo del comando surface: logo de obijuan academy

4 Demo de objetos paramétricos en Python desde Freecad

Video blog 4
(click para ampliar)

Descripción

Demostración de cómo crear objetos usando scripts de python en Freecad, utilizando la biblioteca pyooml

Explicación

Descargarse del github la biblioteca pyooml que de momento se encuentra dentro del proyecto friki. Desde el directorio friki lanzar Freecad

El proyecto Friki en github (click para ampliar)

Creamos un documento nuevo y lanzamos la consola de python desde el menu View / Views / Python Console. Desde la consola pulsamos el botón derecho del ratón y le damos a la opción de "Clear console" para dejar la consola limpia.

Freecad tiene una API en python que nos permite hacer lo mismo que usando los botones de la GUI, y muchísimas más cosas.

(click para ampliar)
(click para ampliar)

Pyooml (Python Object Oriented Mechanics Library) es una biblioteca que usa la API de Freecad para crear objetos muy fácilmente, de manera similar a como se trabaja en Openscad. Primero importamos la biblioteca pyooml con: 

from pyooml import *

Ahora lanzamos un cubo "hola mundo" con el comando cube() 

cube(10, 10, 10)

Nos aparece un cubo tal cual lo hubiésemos lanzado dese el escenario Parts donde al botón del cubo. Tenemos acceso a sus propiedades. Y lo modemos modificar mediante la Gui. Con el método translate() podemos colocar los cubos en cualquier posición: 

cube(10, 10, 10).translate(5,5, 10)
cubo "hola mundo" (click para ampliar)
dos cubos (click para ampliar)

Ahora vamos a hacer uniones de cubos. Primero definimos el vector s para que tenga las dimensiones del cubo: 

 s = FreeCAD.Vector(10,10,10)

Creamos el primer cubo y se lo asignamos a la variable c1: 

 c1 = cube(s)

Ahora el segundo cubo, asignado a la variable c2: 

 c2 = cube(s).translate(s.x/2, s.y/2,0)

Por último hacemos la unión usando el operador +:

pieza = c1 + c2

Se puede ver en el árbol de la izquierda cómo aparece el objeto Union, y dentro los dos cubos

Creando dos cubos (click para ampliar)
Unión de los cubos (click para ampliar)

Vamos a crear una cruz de ejemplo. La creamos mediante una única expresión, haciendo la unión de dos cubos centrados en el origen 

cross = cube(40, 10, 10, center = True) + cube(10, 40, 10, center = True)

Este nuevo objeto lo trasladamos 5mm en el eje z:

cross.transate(0,0,5)

(click para ampliar)
(click para ampliar)

Hacemos una base y la unimos a la cruz para tener la pieza final 

base = cube(50,50,10, center = True)
pieza = cross + base


(click para ampliar)
(click para ampliar)

La verdadera potencia está en ejecutar directamente los scripts. El modo interactivo está muy bien para aprender. Cerramos la consola de python y abrimos el fichero pyooml.py desde la opción del menú file / open

Recolocamos las ventanas con la opción Window / Tile. A la izquierda tenemos el código en python, y a la derecha el visor 3D. Le damos al triángulo verde superior para ejecutar el scripts. Tarda unos minutos en realizar todos los cálculos. Finalmente nos aparecerá el objeto de la figura

(click para ampliar)
(click para ampliar)

5 Trasteando con el BQ Aquaris E4.5 Ubuntu Edition

Video blog 5
Ubuntu phone arrancando (click para ampliar)
Ejecutando un programa en python desde la consola (click para ampliar)

Descripción

Mini demo de mi nuevo teléfono BQ Aquaris E4.5 Ubuntu Edition. Me centro en el aspecto fundamental: el software libre. El kernel se puede compilar y flashear. La gran mayoría de las aplicaciones de la ubuntu store son software libre, por lo que están disponibles las fuentes para poder estudiarlas y modificarlas. Y puedes abrir el Terminal de comandos, e instalar paquetes con apt-get install  :-)

Su belleza está en la libertad

Explicación

Os presento el teléfono BQ Aquaris E4.5 Ubuntu Edition que me acabo de comprar. Se divide en scopes. El scop principal es el que tiene los iconos de las aplicaciones, y donde se encuentra el acceso a la ubuntu store para descargar apps. Hay scopes de noticias, música, vídeos... pero me ha gustado encontrar uno sobre Freecad, donde hay tutoriales. Y entre ellos han puesto los de obijuan academy :-)

El scope de aplicaciones del ubuntu phone (click para ampliar)
Scope de Freecad, con tutoriales (click para ampliar)

Pero al margen de lo que trae y cómo está organizado, y al margen de la funcionalidad... hay algo que destaca sobre el resto de móviles, que es más importe: el software libre. El kernel de linux usado está publicado en este repositorio de github, junto con las instrucciones para compilarlo y "flashearlo" en el móvil. Hay que elegir la rama Aquaris E4.5 Ubuntu-rtm.

Repositorio github del BQ Aquaris E4.5, con las fuentes del kernel de Linux para los ubuntu phones (click para ampliar)
Accediendo al repositorio desde un Ubuntu phone :-) (click para ampliar)

Esta filosofía del software libre está también en las aplicaciones. A diferencia de Android donde la mayoría de las aplicaciones son gratis, aquí la mayoría son LIBRES. Es decir, que están las fuentes disponibles. Que tenemos acceso al conocimiento de cómo están hechas. Por ejemplo vemos la aplicación 100balls, de la tienda. Tiene licencia GPL. Otra es la QT3D Cylinder.

App 100balls. Con licencia GPL :-) (click para ampliar)
App QT3D Cylinder (click para ampliar)

Las fuentes de QT3D Cylinder se encuentran en este repositorio en github

Fuentes de la APP QT3D Cylinder, en github (click para ampliar)

Para cambiar entre las aplicaciones que están lanzadas hay que acceder al borde derecho y tirar hacia la izquierda. Vamos a seleccionar el explorador de archivos, que tiene la misma apariencia que el Nautilus de Ubuntu en el PC

Selecionando entre las aplicaciones abiertas (click para ampliar)
Explorador de ficheros (click para ampliar)

Tirando del borde izquierdo hacia la derecha aparece el lanzador de aplicaciones. Yo ya lo tengo configurado y tengo puesto el terminal de comandos. Por defecto no viene (ya enseñaré en otro videoblog cómo configurarlo). Lo lanzamos y se nos abre la terminal de linux. Ahora es cuando podemos experimentar el poder de nuestro ubuntu phone muajajajajajajaja

Lanzador de aplicaciones para ejecutar el terminal (click para ampliar)
Terminal abierto en un ubuntu phone (click para ampliar)

Desde el terminal vamos a probar algunos comandos: 

$ ls

Aparecen los ficheros que están en nuestro home. Vamos a ver la versión del kernel con: 

$ uname -a

Python NO viene instalado por defecto, pero yo lo tengo instalado. Vamos a ejecutar un programa en python "hola mundo": 

$ python hello.py
Ejecutando comandos en la consola (click para ampliar)
Instalando pip con sudo apt-get install (click para ampliar)

Vamos a instalar el paquete python-pip, que nos permite poder instalar muchos más paquetes python. Lo hacemos mediante este comando: 

$ sudo apt-get install python-pip

Luego comprobamos que está correctamente instalado, ejecutándolo sin argumentos: 

$ pip

Por defecto, en nuestro teléfono ubuntu NO PODEMOS usar apt-get. La imagen grabada es de SOLO LECTURA y al ejecutar este comando obtendremos un error. Para que funcione tenemos que configurar la imagen para que sea tanto de lectura como de escritura. Los detalles los contaré en otro video, pero para los ansiosos os diré que tenéis que tenéis que instalar las utilidades: phablet-tools en vuestro linux y ejecutar el comando: phablet-config writable-image (también es necesario que el teléfono esté configurado en modo desarrollador)

¡Listos para frikear!

6 Configurando el BQ Aquaris E4.5 Ubuntu Edition para frikear

Video blog 6
2015-03-29-Videoblog-6-ubuntu-developer-1.png


Descripción

Configuraremos el ubuntu phone para que podamos frikear con él. Instalaremos la consola y el gestor de archivos

Explicación

Parto del supuesto de que tienes un ubuntu phone en su estado original, recién comprado o flasheado. Asegúrate de que no tienes ningún dato importante. Los pasos a seguir a seguir son:

Paso 1: Entrar en el modo desarrollador

Abrir el lanzador deslizando el borde izquierdo hacia la derecha. Seleccionar el icono de la configuración

Seleccionar icono de configuración en lanzador (click para ampliar)
Pantalla de configuración (click para ampliar)

Nos vamos a la parte inferior de la configuración y buscamos la opción "Acerca de este teléfono". Pulsamos para entrar

Parte inferior del menú de configuración (click para ampliar)
Pantalla de "acerca de este teléfono" (click para ampliar)

Nuevamente nos vamos a la parte inferior y pinchamos en "modo de desarrollador". Activamos la opción Modo de desarrollador. NOTA: El modo desarrollador sólo lo podemos activar si previamente hemos establecido un código o contraseña. Si no es así, debemos pulsar en "Seguridad de bloqueo"

Opción de "modo de desarrollador" (click para ampliar)
Pantalla del modo de desarrollador (click para ampliar)

Usando la opción "codigo de 4 digitos" establecemos el código "1234". Será nuestro pin de frikeo. Ahora ya podemos activar el modo desarrollador

(click para ampliar)
Mode de desarrollador activado (click para ampliar)

Con este modo activado ya nos podemos comunicar desde nuestro PC con el móvil ubuntu, para flashear, instalar paquetes, configurar, etc. Esto lo veremos en el siguiente video

Paso 2: Instalar la APP de Terminal en el ubuntu phone

La terminal de comandos es indispensable. Nos permitirá instalar aplicaciones, ejecutar programas, etc, de manera autónoma en nuestro móvil, sin tener que estar conectados al pc. Aunque es cierto que para desarrollar es infinitamente más cómodo estar conectado al pc. Pero, tener una consola en tu móvil mola. Mola muchísimo :-)

Por defecto la consola NO viene instalada. Para ellos, nos vamos al scope de las aplicaciones. Y arrancamos la tienda de ubuntu (está en la parte inferior)

Scope de las aplicaciones (click para ampliar)
Tienda de ubuntu: en la parte inferior (click para ampliar)

Abrimos el desplegable. La consola está en la categoría de Utilidades. Pinchamos en ellas. En la pantalla bajamos hasta encontrar el terminal. Está muy carca del gestor de archivos, que también instalaremos posteriormente.

Categorías en la tienda (click para ampliar)
El terminal en la tienda (click para ampliar)

Entramos en la página del terminal y pinchamos en el botón de Instalar. Si es la primera vez que instalamos una aplicación en el móvil, tendremos que iniciar sesión en Ubuntu ONE. Introducimos nuestros datos y le damos a Iniciar sesión. Si no tenemos cuentas le damos a "Soy un usuario nuevo de Ubuntu One. Créame una cuenta". Las siguientes veces que queramos instalar una aplicación se nos registrará automáticamente.

Página del terminal (click para ampliar)
Iniciar sesión con Ubuntu One para instalar la App (click para ampliar)

Una vez instalada pulsamos en el botón de Abrir. Nos pedirá que introduzcamos nuestra contraseña. Tecleamos el pin de frikeo "1234" que habíamos configurado antes

Aplicación del terminal instalada (click para ampliar)
Introducir la contraseña para abrir el terminal (click para ampliar)

y... ¡Se nos abre el flamante terminal!!!!! Ya podemos frikear!!! Aunque podemos ejecutar comandos y movernos por los directorios, todavía no podemos instalar con apt-get install. Es necesario configurar la imagen para que sea de lectura/escritura. Lo haremos en el próximo vídeo

Vamos a dejar el terminal en el lanzador. Deslizamos el borde izquierdo para sacar el lanzador. Dejamos pulsado unos sengundos el icono del terminal y pinchamos en la opción anclar. Ahora ya tendremos acceso directo al terminal desde el lanzador.

Terminal abierto en el ubuntu phone (click para ampliar)
Anclando el terminal al lanzador (click para ampliar)

Paso 3: Instalar el gestor de archivos

El gestor de archivos es otra aplicación muy útil. Para instalarla hacemos lo mismo que antes: nos vamos a la tienda y lo encontramos en la categoría del utilidades. Pinchamos y le damos a instalar. Ahora no será necesario iniciar sesión en ubuntu one. Una vez instalado, le damos al botón de abrir. Opcionalmente lo podemos anclar al lanzador, de la misma manera que hemos hecho con el terminal

Listos para instalar el gestor de archivos (click para ampliar)
Gestor instalado y lanzado (click para ampliar)

En el gestor abierto no tenemos acceso de administrador. Para tener acceso total pulsamos en la parte superior derecha y le damos a la opción "Desbloquear acceso". Introducimos nuestra clave (pin de frikeo 1234)

Opción para tener acceso de root (click para ampliar)
Gestor con permisos de root (click para ampliar)

Para ir a un directorio concreto dentro del sistema, tenemos la opción de escribir la ruta. Para ello nos vamos a la pestaña inferior que pone "places" y deslizamos hacia arriba. Nos aparecerá otro gestor de archivos con la opción en la parte superior de introducir la ruta. Introducimos el directorio raiz "/"

Gestor con la opción de escribir la ruta (click para ampliar)
Yendo al directorio raiz (click para ampliar)

Y nos aparecen todos los ficheros de nuestro directorio raiz.

En el directorio raiz (click para ampliar)

Ya tenemos nuestro ubuntu phone listo para trastear con él!!!  :-)

7 Instalacion y configuración de herramientas del escritorio para frikear con el BQ Aquaris E4.5 Ubuntu Edition

Video blog 7
2015-03-29-videoblog-7-1.png


Descripción

Instalaremos las herramientas necesarias en el pc para frikear. Configuraremos la imagen del ubuntu phone en modo lectura / escritura para poder instalar paquetes con apt-get install. Es necesario que el móvil esté configurado en modo desarrollador, como vimos en el videoblog anterior

Explicación

Icono aviso.png DESCARGO DE RESPONSABILIDAD
¡¡¡CUIDADO!! Los comandos que vamos a usar en este video-tutorial pueden ser peligrosos para tu móvil. Tienes que saber lo que estás haciendo. No me hago responsable de cualquier pérdida de datos o daños causados en el móvil. Úsalo bajo tu propia responsabilidad

La documentación oficial de ubuntu para instalarlo en los móviles está disponible en este enlace.

Paso 1: Configuración del repositorio

Configuraremos el siguiente repositorio (PPA), donde se encuentran las herramientas de desarrollo que instalaremos: 

$ sudo add-apt-repository ppa:ubuntu-sdk-team/ppa
$ sudo apt-get update

Paso 2: Instalación de paquetes en el PC

Instalar los siguiente paquetes:

  • Herramienta para flashear:
$ sudo apt-get install ubuntu-device-flash

Adicionalmente nos instalará las herramientas: adb y fastboot

  • Utilidades para trabajar con el móvil conectado por USB: phablet tools:
$ sudo apt-get install phablet-tools

Paso 3: Primera prueba. Tomar un pantallazo

Para comprobar que funciona todo bien vamos a usar la herramienta phablet-screenshot para tomar un pantallazo del ubuntu phone desde nuestro PC:

  • Conectamos el ubuntu phone mediante el cable USB.
  • Nos aseguramos que está desbloqueado (Deslizando la pantalla hacia la izquierda y metiendo el código)
  • Ejecutamos el comando:
$ phablet-screenshot test1.png
Tomando un pantallazo del móvil con phablet-screenshot (click para ampliar)

Toma un pantallazo del móvil y nos lo graba en el directorio del PC desde donde hemos ejecutado el comando phablet-screenshot

Foto del ubuntu phone, en el scope de aplicaciones (click para ampliar)
Pantallazo tomado desde el PC con phablet-screenshot (click para ampliar)

Desde el propio teléfono se pueden tomar pantallazos apretando simultáneamente las teclas de volumen + y -

Paso 4: Accediendo a la línea de comandos desde el PC

A la línea de comandos del móvil podemos acceder a través del terminal que instalamos en el propio móvil en el tutorial pasado, sin embargo, es mucho más cómodo poder hacerlos desde el PC. Para ello ejecutamos el comando phablet-shell: 

$ phablet-shell

La comunicación se hace a través de ssh, por lo que tenemos que tener las claves generadas. Si no es así nos aparecerá este mensaje: 

$ phablet-shell 
 no local key, please run the ssh-keygen command first,
 then run phablet-shell again

Ejecutamos ssh-keygen y le damos al enter en todas las preguntas que nos hace: 

$ ssh-keygen
Generating public/private rsa key pair.
Enter file in which to save the key (/home/obijuan/.ssh/id_rsa): 
Created directory '/home/obijuan/.ssh'.
Enter passphrase (empty for no passphrase): 
Enter same passphrase again: 
Your identification has been saved in /home/obijuan/.ssh/id_rsa.
Your public key has been saved in /home/obijuan/.ssh/id_rsa.pub.
The key fingerprint is:
...

Ahora ya sí que podemos acceder al terminal del móvil con phablet-shell: 

$ phablet-shell 
/home/obijuan/.ssh/known_hosts updated.
Original contents retained as /home/obijuan/.ssh/known_hosts.old
Warning: Permanently added '[localhost]:2222' (RSA) to the list of known hosts.
Welcome to Ubuntu Utopic Unicorn (development branch) (GNU/Linux 3.4.67 armv7l)

* Documentation:  https://help.ubuntu.com/
Last login: Tue Mar 31 15:24:46 2015 from localhost.localdomain
phablet@ubuntu-phablet:~$

Salimos de la consola del movil bien con el comando logout o pulsando Ctrl-D

Accediendo a la línea de comandos del móvil desde el PC (click para ampliar)

Todavía no podemos instalar software con apt-get install. Si lo intentamos nos aparecerá este mensaje de error: 

phablet@ubuntu-phablet:~$ sudo apt-get install python
[sudo] password for phablet: 
W: Not using locking for read only lock file /var/lib/dpkg/lock
E: Unable to write to /var/cache/apt/
E: The package lists or status file could not be parsed or opened.
phablet@ubuntu-phablet:~$

Para solucionarlo hay que poner la imagen en modo de escritura, como se indica en el siguiente paso

Paso 5: Configurar la imagen del móvil en modo escritura

Para poder instalar aplicaciones con apt-get install, es necesario configurar la imagen del móvil para escritura 

$ phablet-config writable-image

El móvil se reiniciará automáticamente para arrancar con la nueva imagen con permisos de escritura. Ahora ya podemos acceder a la consola, bien con phablet-shell o bien desde el propio móvil y empezar a instalar paquetes :-)

Paso 6: Instalando python

Vamos a instalar el intérprete de python para hacer pruebas y comprobar que el apt-get install funciona correctamente. Para ello arrancamos la shell con phablet-shell: 

$ phablet-shell

Ahora instalamos python con: 

phablet@ubuntu-phablet:~$ sudo apt-get install python
Instalando python en el ubuntu phone desde el PC (click para ampliar)
Comprobando que python funciona (click para ampliar)

Listos para frikear!!!!!!!

8 Instalando ubuntu desde 0 en tu BQ Aquaris E4.5 Ubuntu Edition

Video blog 8
Videoblog-08-ubuntu-phone-1.png


Descripción

Explicación de cómo grabar un ubuntu nuevo ("flashearlo") en el BQ Aquaris E4.5 Ubuntu Edition desde 0. El teléfono quedará igual que como estaba al comprarlo

Icono aviso.png DESCARGO DE RESPONSABILIDAD
¡¡¡CUIDADO!! Los comandos que vamos a usar en este video-tutorial pueden ser peligrosos para tu móvil. Tienes que saber lo que estás haciendo. No me hago responsable de cualquier pérdida de datos o daños causados en el móvil. Úsalo bajo tu propia responsabilidad

Explicación

Al frikear con el ubuntu phone, se instalan muchos paquetes, se tocan muchas cosas y en general el móvil queda muy distinto a cómo llegó de fábrica. En este video se muestra cómo "flashear" el teléfono para dejarlo tal y como estaba recién comprado. Por tanto, TODOS LOS DATOS SE PERDERÁN.

Para poder flashear, el paquete ubuntu-device-flash necesita que el teléfono tenga activado adb en el modo "recovery". Los teléfonos recién comprados no tienen esta opción activada. Necesitamos usar una imagen que sí lo tengo activado.

Paso 1: Bajarse la imagen con adb activado en el modo recovery

Bajar la imagen de este enlace:

Paso 2: Apagar el ubuntu phone y reiniciarlo en el modo FASTBOOT

  • Apagamos el teléfono
  • Lo volvemos a encender dejando apretados a la vez el botón de encendido y el de subir el volumen
Botón de encendido y subir volumen en el BQ Aquaris E4.5 ubuntu edition (click para ampliar)
Arrancando el móvil en el modo Boot, apretando a la vez el botón de encendido y el de subir volumen (click para ampliar)
  • Al cabo de unos segundos entramos en el modo de arranque (boot) donde nos aparece un menú de selección del modo de arranque. Con la tecla de SUBIR VOLUMEN desplazamos el cursos hasta la opción de FastBoot y apretamos el botón de BAJAR VOLUMEN para seleccionarlo
En el menú de arranque (click para ampliar)
Modo FASTBOOT seleccionado. ¡Listos para flashear! (click para ampliar)

Paso 3: Flashear la última versión estable de ubuntu touch

Conectamos el teléfono al PC a través del cable USB. En el PC, abrimos un terminal en el directorio donde tenemos descargada la imagen bq-E4_5-ubuntu-recovery.img y ejecutamos este comando: 

$ ubuntu-device-flash touch --channel ubuntu-touch/stable/bq-aquaris.en --bootstrap --recovery-image bq-E4_5-ubuntu-recovery.img

Automáticamente se nos empiezan a descargar los ficheros necesarios de ubuntu (en este caso la última versión estable) y se envían al móvil. Este proceso tarda unos 2 minutos (aunque depende de la conexión de internet que tengamos). Durante esta primera fase aparecerá un logo de ubuntu estático en el centro de la pantalla

Primera etapa del flasheado del ubuntu phone (click para ampliar)
Ejecutando el comando ubuntu-device-flash (click para ampliar)

El programa ubuntu-device-flash termina, aunque el flasheado todavía no. En esta segunda fase aparece un logo de ubuntu girando en sentido horario. El proceso tarda aproximadamente 3 minutos y medio. No tenemos que hacer nada. Sólo esperar.

Transcurrido ese tiempo, el teléfono se reinicia nuevamente y nos aparece el asistente inicial para configurar el teléfono. ¡Ya lo tenemos flasheado!

Segunda fase del flasheado. Logo de ubuntu girando en sentido horario (click para ampliar)
Flasheado completado. El teléfono arranca ejecutando el wizard inicial (click para ampliar)

9 Jugando con vectores en Freecad y Pyooml (Parte 1)

Video blog 9
Video-tut-9-imagen-1.png


Descripción

Freecad tiene una API para trabajar con vectores. En la bibliioteca pyooml se ha añadido el objecto svector() que permite visualizarlos en 3D. De esta forma es muy sencillo hacer operaciones matemáticas con vectores y luego obtener su representación en 3D. Es una herramienta muy útil para aprender sobre vectores, comprobar operaciones, realizar documentaciones, aplicarlo a la cinemática de robots, etc.

Explicación

Para probar los ejemplos que se muestran en el videoblog, primero hay que clonar el proyecto friki que está en el github. Abrimos una terminal y nos situamos en el directorio donde está el proyecto friki. Lanzamos Freecad. De esta forma, podremos importar directamente la biblioteca pyooml desde freecad sin tener que hacer nada adicional.

Proyecto friki en github (click para ampliar)
Lanzando Freecad desde el directorio del proyecto friki (click para ampliar)

Configuramos las ventanas de freecad de forma que la consola de python se nos quede en la parte derecha en vertical. Así podemos ver mejor el historial de comandos.

Freecad con la consola python lista para hacer los ejemplos de vectores (click para ampliar)

Ejemplo 1

FreeCAD incorpora en su API la clase Vector, que nos permite definir vectores y trabajar con ellos. Vamos a importarla escribiendo: 

>>> from FreeCAD import Vector

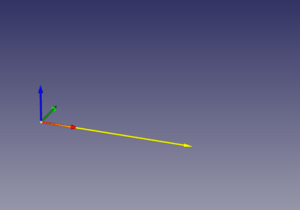
con ella podemos crear vectores matemáticos. Vamos a crear uno: 

>>> v1 = Vector(30, 10, 0)

Podemos acceder a sus propiedades, como por ejemplo su componente x o su longitud: 

>>> v1.x
30.0
>>> v1.Length
31.622776601683793
>>>

En la biblioteca pyooml se ha incorporado el elemento svector (Solid Vector) que permite visualizar los vectores de Freecad. Para visualizar v1 primero importamos la biblioteca pyooml (importamos todo su espacio) y llamamos a svector(v1): 

>>> from pyooml import *
>>> sv1 = svector(v1)

Ahora creamos otro vector (v2) y lo visualizamos también: 

>>> v2 = Vector(10, 30, 0)
>>> sv2 = svector(v2)
Vector v1 visualizado (click para ampliar)
Vector v2 visualizado (click para ampliar)

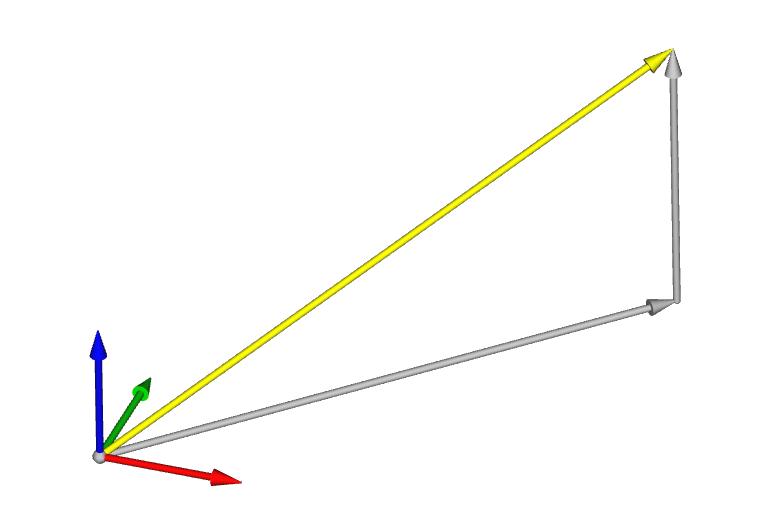
Vamos a sumar los vectores y visualizar el resultado. Creamos el objeto sv3 que dibujará el vector suma: 

>>> sv3 = svector(v1 + v2)

Cambiamos el color a amarillo para distinguirlo de v1 y v2: 

>>> sv3.color("yellow")

Por defecto los vectores se dibujan en el origen. Vamos a trasladarlo al extremo de v1 para visualizar la ley del paralelogramo: 

>>> sv3.translate(v1)
Visualizando el vector suma v1 + v2 (click para ampliar)
Ley del paralelogramo (click para ampliar)

También podemos calcular el producto vectorial de v1 y v2. Será un vector perpendicular al plano formado por v1 y v2. Para visualizarlo mejor, el resultado lo normalizamos y lo multiplicamos por 10 para que esa sea su módulo: 

>>> v4 = v1.cross(v2).normalize() * 10

Ahora los mostramos en 3D, en color azul: 

>>> sv4 = svector(v4).color("blue")

Comprobamos empíricamente que el producto vectorial NO es conmutativo. Si ahora multiplicamos v2 por v1, obtenemos el mismo vector, pero en sentido contrario: 

>>> sv5 = svector( v2.cross(v1).normalize() * 10 )
Visualizando el producto vectorial de v1 x v2 (click para ampliar)
Visualizando el producto vectorial de v2 x v1 (click para ampliar)

Terminamos este ejemplo haciendo una diferencia entre el vector azul (v4) y el amarillo (v1 + v2): 

>>> sv6 = svector ( v4 - (v1 + v2)).color("green")

y lo trasladamos al extremo del amarillo, para ver mejor la diferencia: 

>>> sv6.translate(v1 + v2)
Visualizando la diferencia en verde: v4 - (v1 + v2) (click para ampliar)

10 Jugando con vectores en Freecad y Pyooml (Parte 2)

Video blog 10
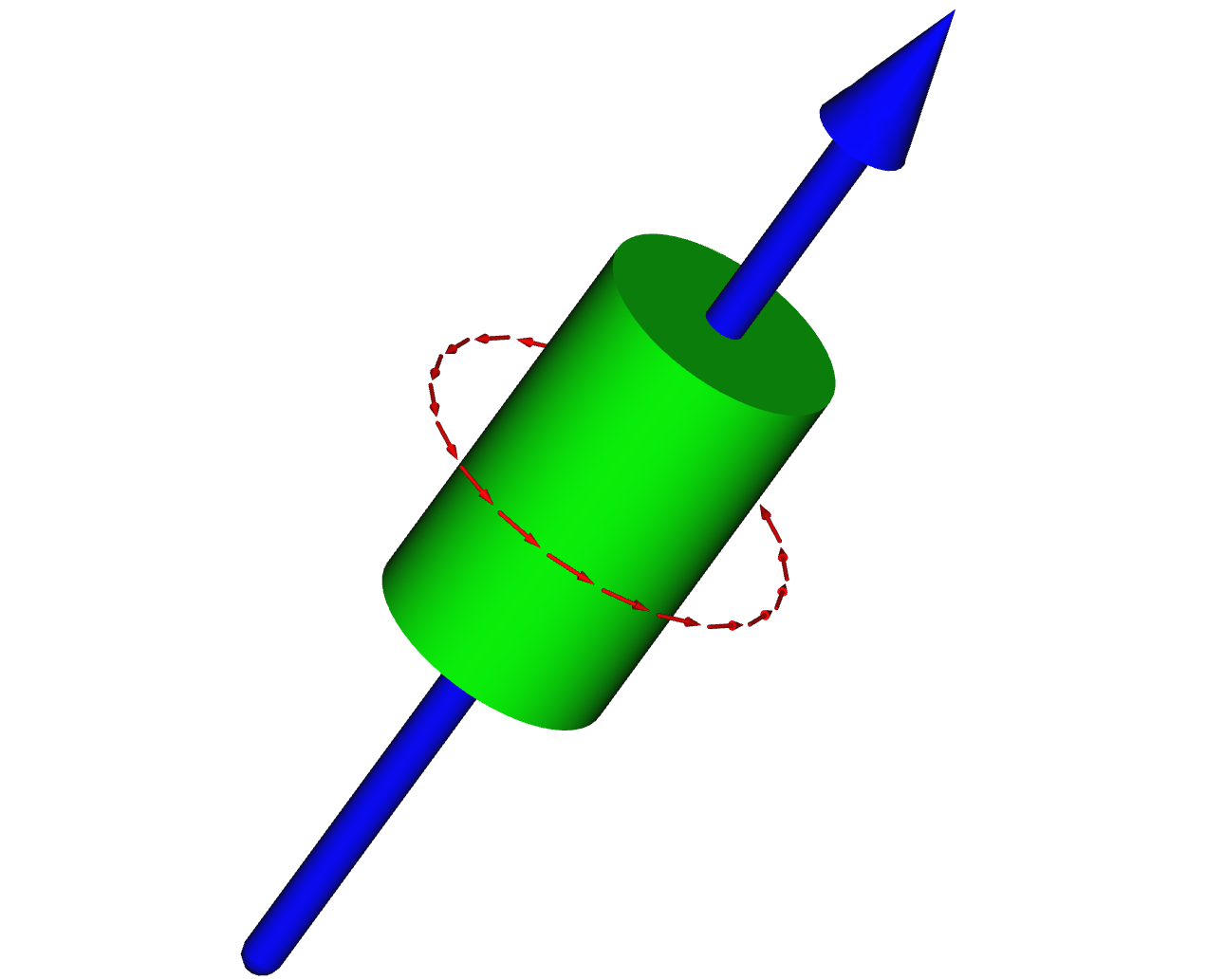
Videoblog-10-exp-0.png


Descripción

Además de vectores, con pyooml también podemos poner puntos y sistemas de referencia. Mediante rotaciones y traslaciones los colocamos donde se necesiten

Explicación

Lazamos freecad desde el directorio donde está el proyecto friki. Abrimos la consola de python. Lo primero que hacemos es cargar las bibliotecas que vamos a usar: 

>>> from FreeCAD import Vector
>>> from pyooml import *

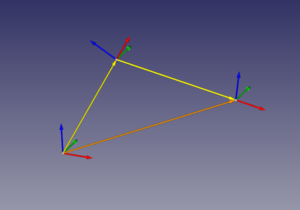
Los sistemas de referencia los visualizamos con la clase frame() de pyooml: 

>>> frame()

Vamos a colocar un punto. Definimos el vector v, y colocamos un punto en esa posición mediante point(): 

>>> v = Vector(10,10,10)
>>> p = point(v)
Sistema de referencia en el origen (click para ampliar)
Visualizando punto en la posición dada por el vector v (click para ampliar)

Mostramos el vector de posición del punto, mediante un vector amarillo: 

>>> sv = svector(v).color("yellow")

Dibujamos un cubo con uno de los vértices en el punto, y lo hacemos transparente con el método ice() 

>>> c = cube(v)
>>> c.ice(80)
Vector de posición del punto (click para ampliar)
Cubo transparente, con uno de los vértices en el punto (click para ampliar)

Creamos otro sistema de referencia: 

>>> f2 = frame()

y lo posicionamos en v: 

>>> f2.translate(v)

Añadimos un tercer sistema de referencia y lo rotamos 30 grados con respecto a su eje x: 

>>> f3 = frame()
>>> f3.rotx(30)
Otros sistema de referencia, en la posición dada por v (click para ampliar)
Sistema de referencia f3, rotado con respecto al inicial (click para ampliar)

Lo situamos en la posición v: 

>>> f3.translate(v)

y lo desplazamos 10mm en dirección del eje de las x:

>>> f3.translate(10,0,0)

Vemos lo fácil que es montar nuestros sistemas de referencia para definir la cinemática de nuestros diseños :-)

Sistema f3 desplazado a la posición v (click para ampliar)
Sistema f3 desplazado una distancia adicional en su eje x (click para ampliar)

Ejemplo 3

En este ejemplo se mostrará un dibujo del campo vectorial magnético a una distancia r provocado por una corriente que circula por un cable. Lo primero es ir a file/open y abrir el script: example-vector-field.py. En vez de ejecutarlo de manera interactiva, como antes, lo vamos a ejecutar de golpe. Le damos al triángulo verde superior. Se nos crea una ventana nueva y al cabo de unos segundos nos aparece el campo vectorial, junto con cable y un vector azul grande que indica el sentido de desplazamiento de la corriente.

Ejemplo de un campo vectorial. Imagen + código (click para ampliar)
Ejemplo del campo vectorial (click para ampliar)

11 Cinemática directa de un brazo robot de 2 grados de libertad con Freecad y Pyooml

Video blog 11
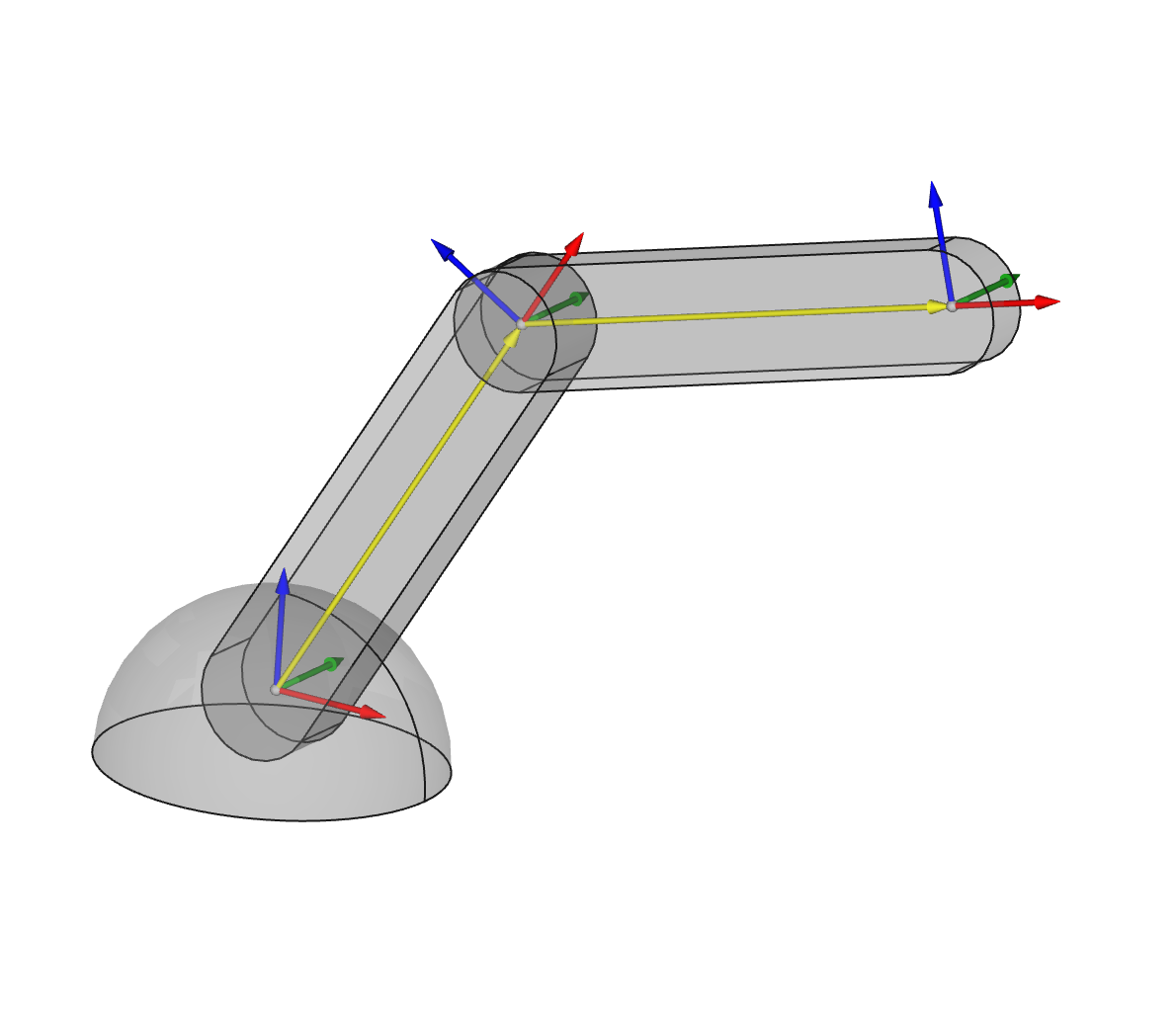
Videoblog-11-exp-0.png


Descripción

Ejemplo de lo fácil que es definir la cinemática directa de un brazo robot con 2 grados de libertad usando Freecad y Pyooml

Explicación

El brazo robot de ejemplo que usaremos es el de la figura 1. Consta de 2 articulaciones de ángulos a1 y a2, unidas mediante dos eslabones de longitudes L1 y L2. En total hay 3 sistemas de referencia: uno en el mundo, y uno en cada extremo de los eslabones.

Arrancamos freecad desde el directorio donde tenemos el proyecto friki y abrimos la consola de python para trabajar de forma interactiva

Fig. 1: Cinemática del robot de 2 grados de libertad (click para ampliar)
Freecad con la consola de python abierta, listo para diseñar la cinemática del robot (click para ampliar)

Importamos las bibliotecas que vamos a usar, como siempre: 

>>> from FreeCAD import Vector
>>> from pyooml import *

Definimos los parámetros de nuestro robot: los ángulos y las longitudes de los eslabones: 

 >>> a1 = -60
 >>> a2 = 70
 >>> L1 = 40
 >>> L2 = 40

Ahora los vectores de los eslabones: 

>>> v1 = Vector(L1, 0, 0)
>>> v2 = Vector(L2, 0, 0)

y los elementos gráficos: 3 sistemas de referencia y 2 vectores sólidos para los eslabones: 

 >>> f0 = frame()
 >>> f1 = frame()
 >>> f2 = frame()
 >>> sv1 = svector(v1).color("yellow")
 >>> sv2 = svector(v2).color("yellow")

Por último definimos las transformaciones, referidas al sistema de referencia móvil: 

 >>> import HMatrix
 >>> Ma = HMatrix.Roty(a1)
 >>> Mb = HMatrix.Translation(v1)
 >>> Mc = HMatrix.Roty(a2)
 >>> Md = HMatrix.Translation(v2)

Empezamos a aplicar las transformaciones a todos los elementos. Primero el vector del eslabón 1: 

 >>> sv1.T = Ma

Le aplicamos la transformación Ma (que es una rotación alrededor del eje y un ángulo a1)

Elementos gráficos creados (superpuestos) (click para ampliar)
Aplicada transformación Ma sobre vector sv1 (click para ampliar)

Colocamos el sistema de referencia f1 al final del eslabón 1, aplicando primero la transformación Ma y luego la Mb. Esto se consigue mediante la multiplicación de las matrices. Estas transformación siempre están referidas al sistema móvil 

>>> f1.T = Ma * Mb

Colocamos el vector del eslabón 2. Aplicamos las transformaciones anteriores más la corresponidente a la rotación de la articulación a2: 

>>> sv2.T = Ma * Mb * Mc
Aplicada transformación Ma * Mb sobre el sistema f1 (click para ampliar)
Aplicada tansformación Ma * Mb * Mc sobre sv2 (click para ampliar)

y el sistema de referencia f2 sobre el extremo del eslabón 2: 

>>> f2.T = Ma * Mb * Mc * Md

La posición del extremo final la obtenemos muy fácilmente multiplicando esta última matriz de transformación por el vector de su origen (0,0,0). Nos devuelve las coordenadas con respecto al sistema del mundo f0. Con esto hemos resuelto la cinemática directa del robot: conocemos en todo momento la posición del extremo final en función de los ángulos a1, a2 y la geometría del robot (l1, l2): 

>>> vr = f2.T.multiply(Vector(0,0,0))
>>> svr = svector(vr).color("orange")
Aplicada transformación Ma * Mb * Mc * Md sobre f2 (click para ampliar)
Cinemática directa resuelta: Vector de posición del extremo (click para ampliar)

Vamos a colocar los eslabones del robot, para que quede más bonito. Primero los creamos. Los hacemos transparentes para poder ver la cinemática: 

>>> l1 = link(l = L1, D = 10, w = 5).ice(80)
>>> l2 = link(l = L2, D = 10, w = 3).ice(80)

Primero es elabón 2. Lo colocamos aplicando la transformación Ma * Mb * Mc 

>>> l2.T = Ma * Mb * Mc
Eslabones creados. Están superpuestos, y situados en el origen (click para ampliar)
Eslabón 2 colocado en su sitio. Definido por la transformación: Ma * Mb * Mc (click para ampliar)

Ahora el eslabón 1. Aplicamos la transformación Ma: 

>>> l1.T = Ma

Para terminar ponemos una base al robot: 

>>> base = sphere(r = 14, angle1 = 0).translate(0, 0, -6).ice(80)
Eslabón 1 colocado (click para ampliar)
Robot final, con su base (click para ampliar)

Ejercicio

Se deja como ejercicio añadir un grado de libertad más en el robot, de manera que el robot completo pueda girar en torno al eje z del sistema de referencia del mundo. La matriz homogenea para hacer esta tansformación es HMatrix.Rotz(angle).

Robot de 3 Grados de libertad (click para ampliar)

12 Proyecto Icestorm: Herramientas libres para sintetizar diseños en FPGAs

Video blog 12

A partir del capítulo 12, la wiki se ha migrado a esta nueva en github

Repositorio

Los ficheros fuentes están en este repositorio:

Enlaces

Autor

Licencia

By-sa.png This work is licensed under a Creative commons Attributions Sharealike.

Créditos

Sobre este VideoBlog

Este videoblog está realizado exclusivamente usando herramientas libres.

  • Sistema Operativo: Ubuntu Linux 14.10
  • Freecad: Freecad 0.14.3702
  • Retoque imagenes: gimp 2.8.10
  • Dibujos: inkscape 0.48.5
  • Grabación escritorio: Kazam 1.4.5
  • Edición de vídeos: Openshot 1.4.3
  • Visualización de las pulsaciones del ratón: keymon 1.17

Noticias

  • 24/Dic/2015: Episodio 12: Migrado a la nueva wiki en github
  • 15/Abril/2015: Episodio 11
  • 12/Abril/2015:
    • Episodio 10
    • Episodio 9
  • 03/Abril/2015: Episodio 8
  • 02/Abril/2015: Episodio 7
  • 29/Marzo/2015: Episodio 6
  • 28/Marzo/2015: Episodio 5
  • 21/Marzo/2015: Episodio 4
  • 19/Marzo/2015: Episodio 3
  • 15/Marzo/2015: Episodio 2
  • 14/Marzo/2015: Subido episodio 1
  • 10/Marzo/2015: Comenzada esta página

Enlaces

Proyecto Clone wars

Proyecto Clone wars: Construye tu impresora 3D opensource!
Proyecto Reprap
 Proyecto RepRap: Impresoras 3D auto-replicantes. El origen de la revolución de las impresoras 3D opensource
Obijuan Academy
Obijuan Academy, Tu academia rebelde! ;-)
Obtenido de «http://iearobotics.com/wiki/index.php?title=Videoblog&oldid=25515»