Diferencia entre revisiones de «Diseño de piezas con Freecad»
(→Participantes) |
(→Participantes) |
||
| Línea 4991: | Línea 4991: | ||
* Tutoriales: 40 | * Tutoriales: 40 | ||
* Ejercicios propuestos: 102 | * Ejercicios propuestos: 102 | ||
| − | * Total de entregas recibidas: | + | * Total de entregas recibidas: 457 |
* Ejercicios enviados: | * Ejercicios enviados: | ||
{| {{tablabonita}} | {| {{tablabonita}} | ||
| Línea 4998: | Línea 4998: | ||
|---- | |---- | ||
| Emilio Jose Morán Hevia | | Emilio Jose Morán Hevia | ||
| − | | | + | |84 |
|---- | |---- | ||
| Bedelber JC | | Bedelber JC | ||
Revisión del 02:46 19 jul 2014
Contenido
- 1 Introducción
- 2 Descargas
- 3 PLAYLIST
- 4 Ejercicios ENTREGADOS
- 5 Empezamos con Freecad!
- 5.1 1) Presentación
- 5.2 2) Cubo Hola mundo!
- 5.3 Propiedades de visualización: En ocasiones veo cubos...
- 5.4 Trasladando cubos: Q*bert
- 5.5 5 La unión hace la fuerza
- 5.6 6 Rotando voy
- 5.7 7 Marcando la diferencia
- 5.8 8 Aplicación: Porta-pendrives
- 5.9 9 Cilindros y Pacman
- 5.10 10 ¡Repíteme!
- 5.11 11 Repetición axial
- 5.12 12 Redondeos, chaflanes y refuerzos
- 5.13 13 ¡Con un par de esferas!
- 5.14 14 Más figuras: usando conos
- 5.15 15 Más figuras: usando toros
- 6 Extrusión de diseños 2D
- 6.1 16 Boceto hola mundo
- 6.2 17 Extrusiones y vaciados
- 6.3 18 Aplicando restricciones
- 6.4 19 Restricciones de simetría
- 6.5 20 Bocetos de polígonos
- 6.6 21 Arcos
- 6.7 22 ¡Qué vienen los recortes!
- 6.8 23 Redondeando bocetos
- 6.9 24 Restricciones externas
- 6.10 25 Extrusión axial
- 6.11 26 Extrusión por trayectoria
- 6.12 27 Interpolación de secciones
- 6.13 28 Hélices y roscas
- 6.14 29: Extrusión con torsión
- 6.15 30 Repeticiones y bocetos
- 6.16 31 Simetría de espejo: espejito, espejito
- 6.17 32 Herramienta de Offset
- 6.18 33 Thickness: Haciendo recipientes
- 7 Trabajando con otros formatos y aplicaciones externas
- 8 Tomas falsas
- 9 Participantes
- 10 Diseños recibidos
- 11 Muro homenaje
- 12 Repositorio
- 13 Autor
- 14 Licencia
- 15 Sobre este tutorial
- 16 Enlaces
- 17 Noticias
Introducción
En esta serie de tutoriales se enseña a hacer diseños 3D desde cero. No se requieren conocimientos previos. El curso está orientado hacia el diseño de piezas que puedan imprimirse en nuestra impresora 3D opensource. La herramienta que usaremos para el diseño es Freecad, aunque las técnicas que aprenderemos nos valdrán para usarlas en otros programas de diseño 3D.
En los tutoriales se proponen ejercicios para que puedas practicar y comprobar por tí mismo tus progresos en el diseño 3D.
| ¡No tengas miedo! ¡Hacer objetos 3D es fácil! ¡Diseña tus propios objetos y materialízalos con tu impresora 3D! ¡Experimenta la increible sensación de convertir tus pensamientos en objetos reales en pocas horas! |
Claves
Tutorial Freecad. Temporada 1. Serie de microtutoriales sobre Freecad, una herramienta de diseño libre y multiplataforma.
Descargas
| Todos los ejemplos están accesibles desde el repositorio en github |
PLAYLIST
| PLAYLIST CON TODOS LOS VIDEOS DE LA TEMPORADA 1 |
|---|
Ejercicios ENTREGADOS
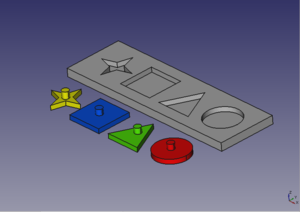
En los tutoriales se han propuesto ejercicios. Aquí están las fotos de las entregas de la gente:
| Album de fotos de las piezas de la parte 1: Empezando con Freecad |
|---|
| Album de fotos de las piezas de las partes 2 y 3: Bocetos y aplicaciones externas |
|---|
Empezamos con Freecad!
1) Presentación
| Video Tutorial 1/40 |
|---|
Descripción
Freecad es una aplicación libre para diseño 3D. Al ser libre, las fuentes están disponibles y cualquier persona o desarrollador tiene acceso a este código para estudiarlo, mejorarlo o compartirlo. La versión que utilizaremos en estos tutoriales es la 0.13.
Ficheros
- Mini-skybot-v2.fcstd: Miniskybot 2
- repyz.fcstd: Módulos REPYZ
Ejercicio propuesto
- Descargar e instalar Freecad 0.13
- Ejecutarlo y juguetear con él
- Abrir el fichero del miniskybot o del módulo REPYZ
2) Cubo Hola mundo!
| Video Tutorial 2/40 |
|---|
Descripción
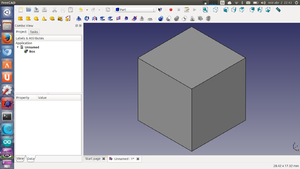
Comenzamos el tutorial. Creación de nuestro primer cubo, usando el workbench parts. Establecimiento de la navegación tipo blender. Cambio en las dimensiones del cubo
Explicación
Ejecutar Freecad. Aparecerá la pantalla de la figura 1.
Crear un documento nuevo (Figura 2). Aparecerá la pantalla de la figura 3
Seleccionar el banco de trabajo parts:
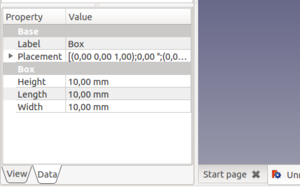
Creamos un cubo (por defecto tiene dimensiones de 10 x 10 x 10 mm)
Activar la perspectiva axonométrica para ver el cubo en 3D:
Pulsando el botón derecho, ir a la opción navigation styles y seleccionar blender:
En este modo de navegación se usa el botón central para mover la cámara. Si además de pulsar este botón se aprieta shift, se desplaza la cámara linealmente a derecha-izquierda y arriba/abajo. Con la rueda del ratón se puede hacer zoom. Con el botón izquierdo se seleccionan objetos. En este enlace hay más información sobre el resto de modos de navegación.
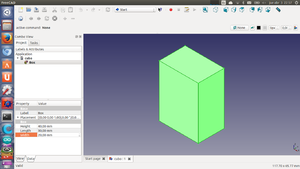
Pulsar en la zona de la derecha en el nombre del cubo creado (box). El cubo cambiará a color verde y en la parte inferior aparecerán 2 nuevas pestañas: View y Data.
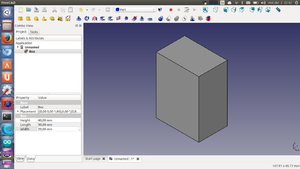
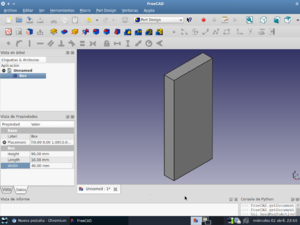
Pulsar en la pestaña data e introducir los valores para las dimensiones del cubo:
Finalmente, ir a File/Export para exportar el cubo a un fichero .stl para que pueda ser impreso en una impresora 3D
Ejercicio propuesto
- Hacer el Monolito de la película 2001 odisea en el espacio. Exportarlo a STL e imprimirlo en 3D.
El primero que lo ha hecho ha sido Xoan Sampaiño (post en G+)
Ficheros
- cubo.fcstd: Cubo hecho en el vídeo tutorial
- ej-monolito.fcstd: Monolito, la solución al ejercicio propuesto
- monolito.stl: Monolito en stl, listo para ser impreso. Dimensiones: 40 x 10 x 90 mm
Propiedades de visualización: En ocasiones veo cubos...
| Video Tutorial 3/40 |
|---|
Descripción
Los objetos en Freecad tienen propiedades, divididas en dos pestañas: data y view. En la pestaña data están las dimensiones del cubo y su posición y orientación. En view todas las relacionadas con la visualización. En este micro-tutorial se explican brevemente.
Explicación
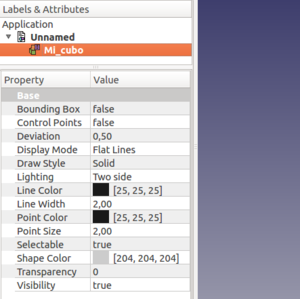
Partimos del cubo hola mundo creado en el tutorial pasado. Cambiamos el nombre a "mi_cubo" pulsando con el botón derecho sobre el nombre "box" en la parte izquierda y luego seleccionando rename.
Ahora mostramos el sistema de referencia pulsando en la opción view/toggle axis cross
Seleccionar el cubo y abrir la pestaña view. Cambiar los modos de visualización seleccionando la opción display. El tipo de línea se cambia con Draw Style. Cambiar los colores del objeto, aristas y vértices con Color Shape, Line color y Point Color respectivamente. La transparencia se modifica con Transparency.
Ejercicio propuesto
- Mediante dos cubos, realizar la composición mostrada en la siguiente figura:
- Entregas de Mizael Gálvez y Carlos cervilla (Cácer):
Ficheros
- T03-cubos.fcstd: Composición de cubos, uno dentro de otro
- T03-ej-base-pilar.fcstd: Solución al ejercicio propuesto
Trasladando cubos: Q*bert
| Video Tutorial 4/40 |
|---|
Descripción
Los objetos en Freecad se trasladan cambiando sus atributos, en la pestaña Data. Como ejemplo se diseña la pirámide de cubos del juego ochentero Q*bert (como homenaje).
Explicación
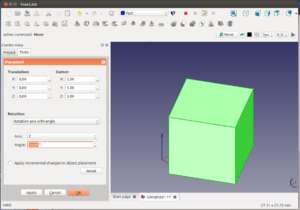
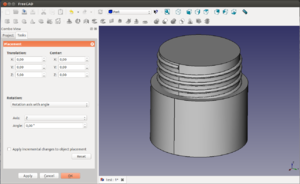
Desde el workbench Parts crear un cubo. Seleccionarlo y pulsar la pestaña Data en sus propiedades. Desplegar la propiedad Placement y dentro la que pone position. Cambiar las coordenadas x,y,z bien introduciendo un valor numérico o bien con la rueda del ratón (para incrementar o decrementar de 1 en 1 mm).
Otra manera de trasladar es accediendo al menú de placement, pinchando en el botón con ... en la parte derecha de placement. Modificar los valores de la posición. Al finalizar pulsar el botón de OK inferior. Si se pulsa en Cancelar, se revocarán los cambios (volviendo al estado inicial).
Otra manera de acceder al placement es através de la opción Edit / placement
Ficheros
- T04-tras-cubos.fcstd: Objetos creados en el tutorial: pirámide de Q*bert de 2 niveles
- T04-ejercicio-1-qbert-3-niveles.fcstd: Solución al ejercicio propuesto: pirámide Q*bert de 3 niveles
Ejercicio propuesto
- Hacer una pirámide de cubos del Q*Bert de 3 niveles
- Entregas de JV. Almodóvar y Carlos Cervilla
5 La unión hace la fuerza
| Video Tutorial 5/40 |
|---|
Descripción
Mediante la unión se construyen piezas más complejas. Al hacer una unión, las piezas originales se mantienen, y la nueva depende de ellas, de manera que si se modifican, la unión también.
Explicación
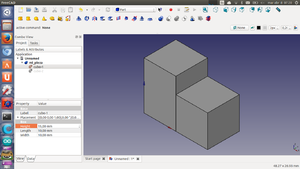
Para hacer la unión de dos cubos primeros hay que seleccionarlos (con la tecla ctrl apretada) y luego pulsar en el icono de la unión. Se crea un nuevo objeto llamado Fusion, que al desplegarlo contiene a los cubos iniciales. Llamaremos a este objeto mi_pieza.
Si ahora modificamos las dimensiones de los cubos originales, también se modificará mi_pieza.
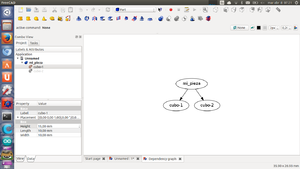
Esta relación de dependencia la podemos ver gráficamente pinchando en la opción tools/dependency graph (Es necesario tener instaladas las librerías graphviz)
Por defecto, Freecad NO hace un refinado de las geometrías, de manera que hay aristas que realmente ya no lo son (lo eran en los objetos antes de hacer la unión). Para hacer este refinado hay que pinchar en la opción part/refine shape.
Este refinado se puede hacer automáticamente cada vez que se ejecute una unión (o cualquier otra operación booleana). Hay que ir a Edit/preferences. En la opción de "Part Design" activar las dos casillas.
Ejercicios propuestos
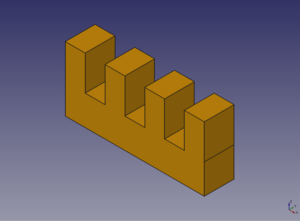
- Ejercicio 1: Rehacer la pirámide del QBert de 2 niveles, usando uniones (y refinando las geometrías)
- Ejercicio 2: Idem pero con la pirámide del QBert de 3 niveles
- Ejercicio 3: Diseñar las piezas del tetris usando uniones de cubos de 10mm
- Entregas de Fernando Remiro, JV Almodóvar y Carlos Cervilla:
Ficheros
- Pieza diseñada en el tutorial: T05-union.fcstd
- Ejercicio 1: T05-ej1-qbert-2-niveles.fcstd (qbert-2.stl)
- Ejercicio 2: T05-ej2-qbert-3-niveles.fcstd (qbert-3.stl)
- Ejercicio 3: T05-ej3-piezas-tetris.fcstd (piezas-tetris.stl)
6 Rotando voy
| Video Tutorial 6/40 |
|---|
Descripción
Las rotaciones de objetos se realizan en el mismo menú placement que las traslaciones. Por defecto se aplican sobre el origen del objeto, pero se puede especificar otro centro para.
Explicación
Partimos de un cubo "hola mundo". Para realizar rotaciones seleccionamos el cubo y vamos al menú de placement (igual que con las traslaciones), en la pestaña DATA / placement. Seleccionamos el eje Z y los grados. Pulsamos OK
Para cambiar el eje de rotación para que el cubo gire respecto a su centro por ejemplo, ponemos las coordenadas del origen del nuevo sistema de referencia en CENTER.
Vamos a crear como ejemplo una X formada por dos paralelepípedos. Primero colocamos uno de dimensiones 10 x 2 x 2 mm y lo rotamos -20 grados con respecto a su centro. Luego lo duplicamos con la opción edit / duplicate selection. En este nuevo objeto, abrimos el menú de placement, hacemos un Reset y lo rotamos 20 grados con respecto a su centro, obteniendo la X
Dos objetos independientes se pueden mover y rotar. Para ello los seleccionamos y abrimos el menú de placement. Allí activamos la opción "Apply incremental changes" y aplicamos las rotaciones y traslaciones que necesitemos. Si queremos que el centro de referencia de la X esté en su centro geométrico, movemos la X hasta que su centro coincida con el eje z del sistema de referencia global y realizamos la unión. Ahora la X se podrá rotar y trasladar como un objeto cualquiera. Las rotaciones se aplicarán con referencia a su centro.
Ejercicio propuesto
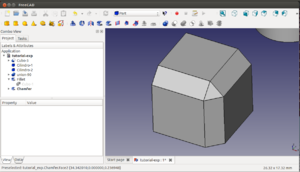
- Hacer una casa como la mostrada en la siguiente figura. Está formada por dos paralelepípedos, uno rotado y trasladado
- Entrega de JV. Almodóvar:
Ficheros
- rotaciones.fcstd: Ejemplo mostrado en el tutorial: la X
- T06-ej-casa.fcstd: Solución al ejercicio: la casa
7 Marcando la diferencia
| Video Tutorial 7/40 |
|---|
Descripción
La operación booleana de diferencia es muy importante. Se utiliza muchísimo. Con ella sustraemos a un objeto una parte, lo que nos permite hacer taladros, vaciados, etc.
Explicación
Partimos de dos cubos de 10mm de arista, uno de ellos trasladado a la posición (5, -5, 5). Seleccionamos primero el cubo original y luego el trasladado (Pulsando la tecla control). Para hacer la diferencia pinchamos en el icono 
Se realizará la diferencia. El nuevo objeto se denomina Cut. Pinchar sobre él y renombrarlo a "mi_pieza". Si pinchamos en la opción Tools/ Dependency graph aparecerá las relaciones entre los objetos creados. Mi_pieza depende de los dos cubos. Si modificamos uno de ellos, automáticamente se actualizará mi_pieza. Comprobarlo modificando la traslación del segundo cubo, llevándolo a la posición (2,-2,2)
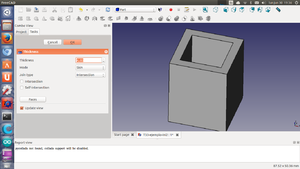
Ejercicio propuesto
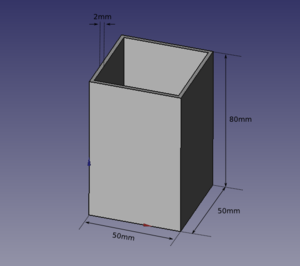
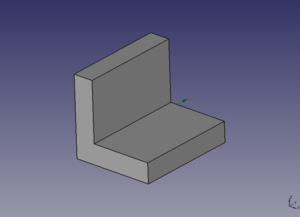
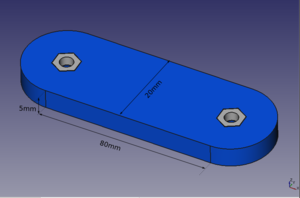
- Hacer un portalápices que tenga unas dimensiones de 50 x 50 x 80 mm y un espesor de 2mm en las paredes laterales y fondo de 3mm
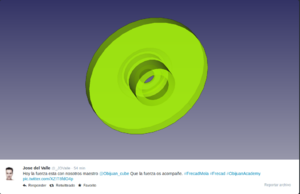
- Entregas de los ejercicios de Jose del Valle (@_JDValle) y Federico Coca (@fgcoca)
Ficheros
- T07-diferencia.fcstd: Pieza mostrada en el videotutorial
- T07-ej1-portalapices.fcstd: Solución al ejercicio: un portalápices
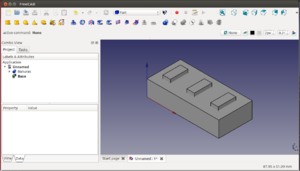
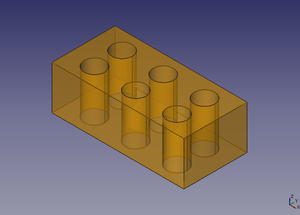
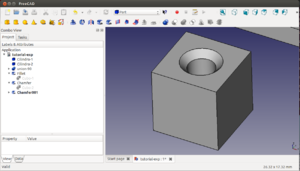
8 Aplicación: Porta-pendrives
| Video Tutorial 8/40 |
|---|
Descripción
Vamos a aplicar todos los conocimientos aprendidos hasta ahora diseñando un porta-pendrives. Con sólo conocer cómo hacer traslaciones, rotaciones, uniones y diferencias, y cómo construir cubos, ya podemos hacer cantidad de piezas 3D muy útiles, que luego podremos imprimir en una impresora 3D.
Explicación
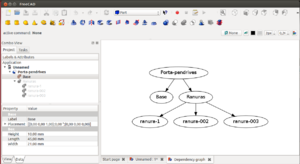
Comenzamos definiendo los huecos de las ranuras. Creamos un cubo de dimensiones: (4.7, 11, 12) y lo llamamos ranura-1. Lo duplicamos dos veces para obtener 3 cubos iguales (ranura-2 y ranura-3). Dos de ellos los desplazamos a lo largo del eje x. Los seleccionamos todos y hacemos su unión, que renominaremos con el nombre de ranuras.
Creamos otro cubo, de dimensiones (45, 21, 10), y lo llamamos base. Los desplazamos a la posición (-5, -5, 0) para que las ranuras queden centradas.
Seleccionamos la base y las ranuras y los trasladamos de manera que el sistema de referencia global quede en una de sus esquinas. A continuación seleccionamos primero la base y luego las ranuras y hacemos la diferencia. Ya tenemos listo nuesto porta-pendrive!!
Finalmente podemos visualizar las dependencias entre las diferentes partes del objeto:
Ejercicio propuesto
- Hacer un porta-tarjetas sd, con capacidad para 4.
- Entregas de Adolfo Castaño (@adocasma) y Federico Coca (@fgcoca)
Ficheros
| T08-porta-pendrives.fcstd | El porta-pendrives (Freecad) |
| T08-portapendrives.stl | El porta-pendrives, en STL |
| T08-porta-sd.fcstd | El porta-SDs (Freecad) |
| T08-porta-sd.stl | El porta-SDs, en STL |
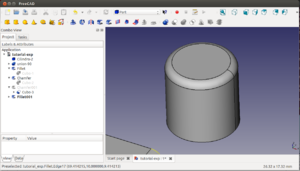
9 Cilindros y Pacman
| Video Tutorial 9/40 |
|---|
Descripción
Los cilindros son otro de los objetos básicos que nos permiten modelar muchísimas piezas a partir de ellos. También se usan mucho para realizar taladros y vaciados, mediante diferencias.
Explicación
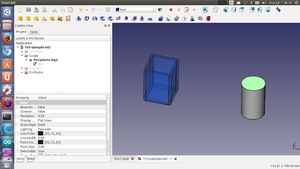
Vamos a crear nuestro primer cilindro "hola mundo". Para ello, en el banco de pruebas part, en la parte superior pinchamos en el icono que tiene dibujado un cilindro. Nos aparecerá un cilindro nuevo, centrado en el ele z y apoyado en el plano xy, de 4mm de diámetro y 10mm de altura.
El cilindro tiene 3 parámetros: el radio, la altura y el ángulo. Por defecto se obtiene un cilindro con ángulo de 360 grados, pero se pueden especificar sectores reduciéndolo. Para construir un pacman establecemos el radio a 25mm y la altura a 5mm. Cambiamos el ángulo a 270 grados para convertirlo en un sector circular. A continuación lo rotamos 45 grados alrededor del eje z para que la boca se centre y apunte hacia el lado positivo del eje x
Creamos un cilindro nuevo de 10mm de altura y radio de 1.5mm que se convertirá en el ojo del pacman. Lo desplazamos -2mm en el eje z y 10mm en el y. Seleccionamos primero la cara y luego este nuevo cilindro y aplicamos una diferencia. Es el momento de cambiar el color a amarillo y ¡ya tenemos nuestro pacman!
Los cilindros ya no tienen secreotos para nosotros ;-)
Ejercicios propuestos
- Ejercicio 1: La tarta
- Ejercicio 2: Un ladrillo
- Entregas de Xoan Sampaiño (@xoan) y JV Almodóvar
Ficheros
| T09-pacman.fcstd | El pacman de ejemplo, en freecad |
| pacman.stl | El pacman de ejemplo, en STL |
| T09-tarta.fcstd | Una tarta cortada, en freecad |
| pie.stl | Una tarta cortada, en STL |
| T09-brick.fcstd | Un ladrillo, en Freecad |
| brick.stl | Un ladrillo, en STL |
10 ¡Repíteme!
| Video Tutorial 10/40 |
|---|
Descripción
Muchas piezas se construyen mediante la repetición espacial de sus componentes. Mediante "los arrays" podemos copiar y posicionar objetos.
Explicación
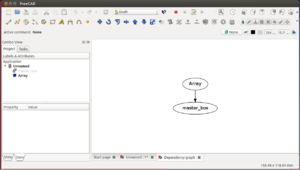
Desde el entorno part creamos un cubo de 10x10x10 que nombramos como master_box. Nos vamos al entorno draft y allí pulsamos en el icono de creación de arrays 
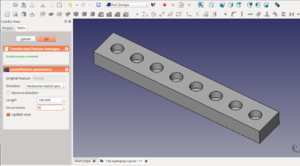
Nos aparecerá un nuevo objeto denominado Array (y la master_box se hará invisible). Lo seleccionamos y nos vamos a la pestaña data de sus propiedades. Allí ponemos la propiedad NUMBER Y a 1, ya que solo queremos repetición en el eje de la X (en este ejemplo). A continuacion desplegamos la propiedad Interval X y ponemos el valor 12 en x. Aparecerá un segundo cubo, clon de master_box, desplazado 12mm en el eje de las x.
Ahora queremos colocar 10 cubos, por lo en la propiedad Number x ponemos 10. Aparecerán 10 repeticiones del cubo original a lo largo del eje x. Este array depende del cubo original. Esto lo podemos ver mostrando las dependiencias en la opción tools / dependency graph. Si modificamos algún parámetro del cubo original, automáticamente se modificará en el resto de cubos.
Desde el entorno parts, creamos un cubo nuevo, de dimensiones (122, 16, 3) y lo desplazamos a la posición (-2,-2,4). Lo llamaremos base_1D. Lo seleccionamos, luego el array y hacemos la diferencia. Se crea un nuevo objeto que llamaremos pieza_1D
Este objeto depende en última estancia de master_box. Si cambiamos, por ejemplo, su anchura a 12mm, la pieza_1D también cambiará.
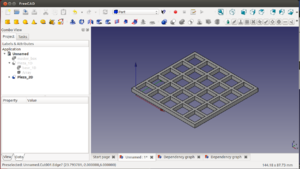
Ahora hacemos invisible la pieza_1D. Vamos a crear un array bidimensional con el mismo cubo inicial (master_box). Para ello seleccionamos el cubo y volver a darle al botón de crear array (en el banco de trabajo draft). Desplegamos interval x: asignamos x = 12. Desplegamos interval y: asignamos y = 12. Por último asignamos Number x = 5, y Number y = 5.
Creamos un cubo nuevo, llamado base_2D, con dimensiones (62, 62, 3) y lo posicionamos en (-2, -2, 3). Ahora hacemos la diferencia para obtener la pieza_2D.
Hacemos invisible la pieza_2D, y creamos un nuevo array, pero esta vez tridimensional. Hacemos lo mismo que en el caso anterior, pero ahora desplegamos también interval z y asignamos z = 12. Asignamos también Number z = 5.
Por último creamos un cubo interior, de dimensiones (54,54,54). Lo posicionamos en (2,2,2). Le restamos el nuevo array tridimensional. Obtenemos la pieza_3D
Diagrama de dependencias final:
Ejercicios propuestos
- Ejercicio 1: Crear una pieza de mecano de 5x1, usando la repetición
- Ejercicio 2: Construir la torre de un castillo, con sus almenas, usando la repetición
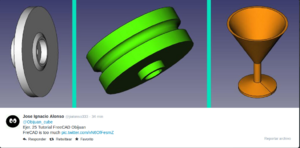
- Entregas de Jose Ignacio Alonso y Jose Carlos Carmona
Ficheros
| T10-array_1D.fcstd | Pieza con repetición a lo largo del eje x |
| T10-array_2D.fcstd | Pieza con repetición en 2D |
| T10-array_3D.fcstd | Pieza con repetición en 3D |
| T10-ej1-pieza_mecano.fcstd | Pieza de mecano, en freecad |
| T10-ej1-pieza-mecano.stl | Pieza de mecano, en STL |
| T10-ej2-castillo.fcstd | Torre del castillo, en Freecad |
| T10-ej1-castillo.stl | Torre del castillo, en STL |
11 Repetición axial
| Video Tutorial 11/40 |
|---|
Descripción
Las repeticiones de elementos se pueden hacer también de manera que roten alrededor de un centro. Esto permite crear fácilmente taladros y huecos en elementos circulares
Explicación
Partimos del cubo hola mundo, desplazado a la posición (20, -5, 0). Crearemos copias de él dispuestas alrededor del eje z. Seleccionamos al cubo y pinchamos en el icono de crear arrays en el banco de trabajo draft (igual que en el tutorial anterior). Ahora, en las propiedades, establecemos Array Type a Polar.
Establecemos la propiedad Number a 6. Nos aparecerán 6 cubos, equiespaciados angularmente, resultado de la rotación de 360 grados del cubo original alrededor del origen. Se puede establecer otro ángulo. Si por ejemplo sólo se quiere que los cubos recorran 180 grados, establecer la propiedad Angle a 180 grados
Como ejemplo vamos a construir una brida de empalme de tuberías. Creamos primero un cilincro de 60mm de diámetro y 5mm de altura. Luego creamos el tubo exterior: otro cilindro de 30mm de diámetro y 12mm de altura. Hacemos la fusión de los dos.
Hacemos un tercer cilindro que será el interior del tubo: 20mm de diámetro y 30mm de altura y se lo restamos al objeto anterior. Obtenemos la brida sin taladros. Creamos un cilindro que usaremos de broca para taladrar: 6mm de diámetro, colocado en la posición (22, 0, -1)
Seleccionamos el taladro y lo repetimos axialmente. Luego realizamos la resta de la brida con los taladros. Ya tenemos el objeto final terminado.
Ejercicios propuestos
- Ejercicio 1: Botón giratorio
- Ejercicio 2: Ficha del trivial (Idea de Paco Malpartida)
- Ejercicio 3: Torre de un castillo
- Entregas de Jose Ignacio Alonso (@jialonso333) y JV Almodóvar
Ficheros
| T11-brida-empalme.fcstd | Brida de empalme de tuberías. Freecad |
| T11-brida-empalme.stl | Brida de empalme de tuberías. STL |
| T11-ej1-boton-giratorio.fcstd | Botón giratorio. Freecad |
| T11-boton-giratorio.stl | Botón giratorio. STL |
| T11-ej2-quesitos-trivial.fcstd | Ficha del trivial. Freecad |
| T11-ficha-quesitos-trivial.stl | Ficha del trivial. STL |
| T11-ej3-castillo2.fcstd | Torre del castillo. Freecad |
| T11-torre-castillo2.stl | Torre del castillo. STL |
12 Redondeos, chaflanes y refuerzos
| Video Tutorial 12/40 |
|---|
Descripción
Sobre las aristas de cualquier objeto se pueden aplicar redondeos y chaflanes. Además, si la arista es interior, lo que se obtienen son refuerzos
Explicación
Partimos de unas figuras iniciales a las que aplicaremos los redondeos, chaflanes y refuerzos
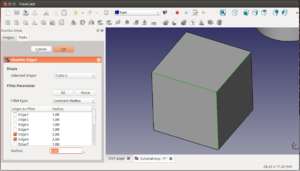
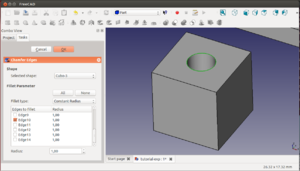
Seleccionamos el cubo-1 en la vista 3D y pulsamos el botón derecho para desplegar el menú. Ahí le damos a la opción "fit selection" para centrar la vista 3D en el cubo 1. Ahora seleccionamos las aristas que queremos redondear. Por ejemplo las 3 aristas que salen de uno de los vértices superiores (ver figura). Para ello selecionamos la primera con el ratón (se pondrá en verde) y las otras dos dándole a cntrl + botón izquierdo del ratón (la selección depende del modo de navegación que estemos usando. En mi caso uso la navegación Blender). Luego pinchamos en el icono de redondeo (fillet) 
Se nos aparecerá una ventana en la parte izquierda con las aristas (edges) y los radios de redondeo a aplicar. Nos vamos a la casilla radius y ponemos por ejemplo 2. Le damos al ok en la parte superior y ..... ¡Ya tenemos los bordes redondeados!
Ahora vamos a aplicar chaflanes a 3 aristas del cubo 2. Repetimos la operación: centramos el cubo 2 en la vista 3D, igual que antes. Seleccionamos las aristas a aplicar el chaflán. Por ejemplo las mismas que con el cubo 1. Le damos al icono de hacer chaflanes (chamfer) 
. Se nos abre otro menú donde podemos seleccionar el radio del chaflán. Vamos a poner 2mm por ejemplo. Al darle ok nos aparecerá el nuevo cubo.
Los chaflanes y redondeos también se pueden hacer en bordes no rectos, como los circulares que tiene el cubo 3. Seleccionamos el borde circular, pulsamos en el icono de chaflán, indicamos un radio de 1mm y pulsamos ok.
También lo podmeos aplicar a los bordes exteriore de los cilindros (objetos convexos)
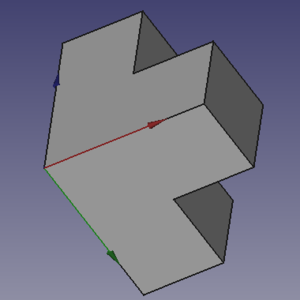
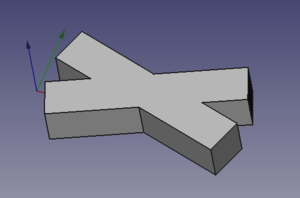
Los chaflanes y redondeos se pueden aplicar en figuras no convexas para crear refuerzos en las uniones a 90 grados. La forma de hacerlo es la habitual: se selecciona la arista de unión entre las dos caras perpendiculares y se aplica un chaflán o un redondeo. En la figura de ejemplo aplicaremos ambas, una a cada lado.
Ejercicios propuestos
- Ejercicio 1: Botón con chaflán en la parte superior y con hendiduras que no lleguen hasta la base (Idea de JV. Almodóvar)
- Ejercicio 2: Tableta de chocolate de 5 x 4 onzas
- Ejercicio 3:
- Entregas de Alfonso López y Jose Ignacio Alonso (@jialonso333)
Ficheros
| T12-tutorial-ini.fcstd | Objetos iniciales sobre los que hacer el tutorial 12 (Freecad) |
| T12-chaflan-redondeo.fcstd | Piezas de ejemplo, mostradas en el tutorial (Freecad) |
| T12-ej1-boton.fcstd | Ejercicio 1: Botón (Freecad) |
| T12-ej1-boton.stl | Ejercicio 1: Botón (STL) |
| T12-ej2-chocolate.fcstd | Ejercicio 2: Tableta de Chocolate (Freecad) |
| T12-ej2-chocolate.stl | Ejercicio 2: Tableta de Chocolate (STL) |
| T12-ej3-pieza.fcstd | Ejercicio 3: Pieza de soporte (Freecad) |
| T12-ej3-soporte.stl | Ejercicio 3: Pieza de soporte (STL) |
13 ¡Con un par de esferas!
| Video Tutorial 13/40 |
|---|
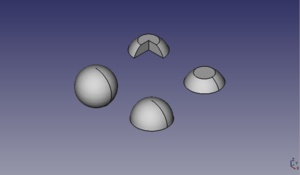
Descripción
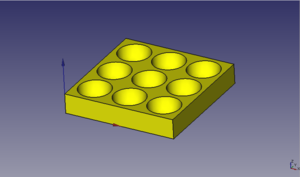
Aprenderemos a hacer esferas y ver cuáles son sus parámetros. Como ejemplo haremos un portacanicas para guardar 9 canicas
Explicación
Las esferas se crean usando el icono amarillo con una esfera 
en el banco de trabajo part.
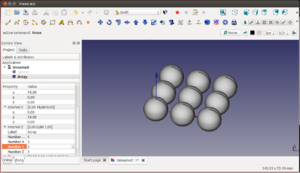
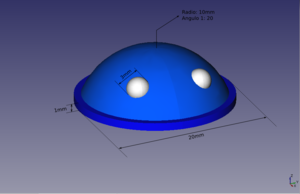
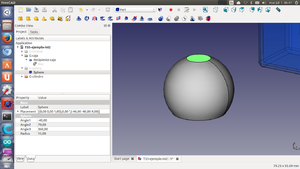
Las esferas tienen 4 propiedades importantes, accesibles desde la pestaña DATA: radio, ángulo 1, ángulo 2 y ángulo 3. El ángulo 1 determina la posición del plano inferior de corte de la esfera. En las figuras se muestra un valor de este ángulo de 0 grados (correspondiente a una semiesfera) y de 20 grados (zona esférica):
El ángulo 2 determina la posición del plano superior de corte para hacer una zona esférica. En las figuras el valor se ha fijado a 60 grados. Finalmente, el ángulo 3 determina la rotación a lo largo del eje z. En la figura se ha puesto a 270 grados
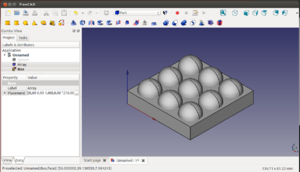
Como ejemplo de uso de las esferas vamos a hacer un portacanicas, para poder colocar 9 canicas. Hacemos primero una esfera de 8mm de radio y usando la repetición creamos un array de 3 x 3 esferas, dejando 2mm de espacio entre ellas. A continuación hacemos la base, con unas dimensiones de 56 x 56 x 10 mm.
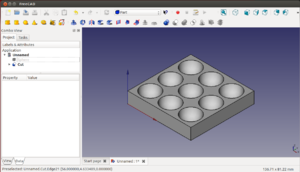
Movemos la base para que las esferas queden centradas y que sólo sobresalgan las semiesferas. Luego movemos tanto la caja como las esferas para situar el origen de referencia en una de las esquinas inferiores de la caja. Por último hacemos la diferencia entre la base y las esferas para obtener nuestro portacanicas.
Ejercicios propuestos
- Ejercicio 1: Cabeza de robot
- Ejercicio 2: Dado
- Ejercicio 3: Ficha de dominó
- Entregas de Jose María Martín y Jose Ignacio Alonso (@jialonso333)
Ficheros
| T13-esferas-portacanicas.fcstd | Portacanicas (Freecad) |
| T13-esferas-portacanicas.stl | Portacanicas (STL) |
| T13-ej1-cabeza-robot.fcstd | Cabeza de robot (Freecad) |
| T13-ej1-cabeza-robot.stl | Cabeza de robot (STL) |
| T13-ej2-dado.fcstd | Dado (Freecad) |
| T13-ej2-dado.stl | Dado (STL) |
| T13-ej3-dominio.fcstd | Ficha dominó (Freecad) |
| T13-ej3-ficha-domino.stl | Ficha dominó (STL) |
14 Más figuras: usando conos
| Video Tutorial 14/40 |
|---|
Descripción
Creación de conos y conos truncados. Los conos tienen 4 parámetros: radio de la base, radio superior, altura y ángulo de revolución.
Explicación
Para crear nuestro primer cono, nos vamos al banco de trabajo part y le damos al icono de crear conos 
. En la pestaña de DATA vemos la propiedades del cono, que son 4: altura, radio1, radio2 y ángulo de revolución. Con radius1 cambiamos el radio de la base inferior. Lo pondremos a 10mm
Con radius2 modificamos el de la base superior. Lo ponemos a 1mm. Si se pone a 0mm tendremos un cono perfecto (y no truncado). Con angle cambiamos el ángulo de revolución. Lo ponemos por ejemplo a 270 grados para ver su efecto.
Vamos a crear un vaso de ejemplo, usando conos. Creamos un cono con los siguientes parámetros: radius1 = 15, radius2 = 25, height = 70. Este será el cono que define el exterior del vaso. A continuación lo duplicamos (edit/duplicate selection) y modificamos los radios para que sean 2mm menores: radius1 = 13, radius2 = 23. Con esto conseguimos que el ancho de la pared del vaso sea de 2mm.
El cono interior su desplazamos 2mm a lo largo del eje z, de manera que sobresalga sobre el otro. Seleccionamos el exterior, luego el interior y hacemos la diferencia para vaciarlo por dentro.
Ahora redondeamos los dos bordes superiores (interior y exterior), dándoles un radio de redondeo de 1mm. Finalmente lo dejamos con un 50% de transparencia, para ver el interior
Ejercicios propuestos
- Ejercicio 1: Tornillo M4 de cabeza cónica
- Ejercicio 2: Cono de tráfico
- Ejercicio 3: Embudo
- Entregas de Alfonso López y Jose Ignacio Alonso (@@jialonso333)
Ficheros
| T14-vaso.fcstd | Vaso de ejemplo (Freecad) |
| T14-vaso.stl | Vaso de ejemplo (STL) |
| T14-ej1-tornillo.fcstd | Tornillo de cabeza cónica (Freecad) |
| T14-ej2-cono-trafico.fcstd | Cono de tráfico (freecad) |
| T14-ej2-cono-trafico.stl | Cono de tráfico (STL) |
| T14-ej3-embudo.fcstd | Embudo (Freecad) |
| T14-ej3-embudo.stl | Embudo (STL) |
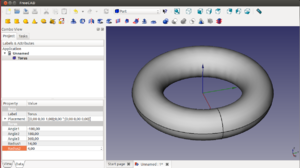
15 Más figuras: usando toros
| Video Tutorial 15/40 |
|---|
Descripción
Creación de toros. Tienen varias propiedades principales: el radio de la sección, el radio del toro y el ángulo de revolución.
Explicación
Creamos un toro hola mundo desde el banco de trabajo part pulsando el icono amarillo que tiene un toro 
. El radio del toro se cambia con la propiedad radius1. La ponemos por ejemplo a 14mm, para agrandarlo.
El radio de la sección del toro se cambia con radius2. Lo aumentamos a 4. El parámetro angle3 es el ángulo de revolución del toro. Por defecto este ángulo está a 360 grados (toro cerrado). Cualquier valor menos hará que quede abierto. Lo ponemos como ejemplo a 270 grados.
Los otros dos ángulos (angle1 y angle2) determinan los ángulos de los semitoros superior e inferior. Sin embargo, al modificar estos valores, el toro deja de ser un objeto sólido, y se convierte en una superficie.
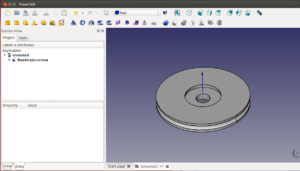
Como ejemplo de aplicación de uso del toro, vamos a crear la rueda del printbot Miniskybot 2. Primero creamos un cilindro de 6mm de altura y radio de 28mm. Lo denominamos rueda base. A continuación creamos un toro que nos servirá para hacer la hendidura por la que va la junta tórica que hace de neumático en la rueda. El radio del toro es el mismo que el de la rueda: 28mm y el radio de su sección es de 1.5mm. Lo renombramos a hueco-junta-tórica
Ahora restamos la junta tórica a la rueda para crear el hueco. Lo llamamos rueda básica. Para hacer el hueco de la corona del servo, usamos un cilindro de 10.9mm de radio. Lo movemos para que penetre por la parte superior de la rueda una distancia de 2mm y se lo restamos.
Colocamos un cilindro de 4.35mm de radio y lo restamos, para hacer el hueco para el eje del servo. Por último hay que hacer los taladros donde irá la corona del servo. Ponemos un cilindro de 0.75mm de radio, que atraviese la rueda. Lo desplazamos a la posición x = 7.3 y hacemos un array axial de 4
Hacemos la resta y... ¡Ya tenemos nuestra rueda lista!
Ejercicios propuestos
- Ejercicio 1: Smiley!
- Ejercicio 2: Portacanicas
- Ejercicio 3: Patas para mesa de ikea
- Entregas de Jose Ignacio Alonso @jialonso333 y Alfonso López
Ficheros
| T15-miniskybot-wheel.fcstd | Rueda del miniskybot (Freecad) |
| T15-miniskybot-wheel.stl | Rueda del miniskybot (STL) |
| T15-ej1-smiley.fcstd | Smiley (Freecad) |
| T15-ej1-smiley.stl | Smiley (STL) |
| T15-ej2-portacanicas-toro.fcstd | Portacanicas (Freecad) |
| T15-ej2-portacanicas.stl | Portacanicas (STL) |
| T15-ej3-pata-mesa-ikea.fcstd | Pata mesa ikea (Freecad) |
| T15-ej3-pata-mesa-ikea.stl | Pata mesa ikea (STL) |
Extrusión de diseños 2D
16 Boceto hola mundo
| Video Tutorial 16/40 |
|---|
Descripción
En los tutoriales del 1 al 15 hemos estado usando geometría constructiva para crear nuestras piezas. Consiste en combinar figuras básicas (cubos, cilindros, esferas, toros...) mediante las operaciones booleanas (unión, resta, intersección).
Además de la geometría constructiva, en Freecad se pueden crear piezas mediante la extrusión de dibujos 2D. Creamos un plano de una sección de la pieza y la extruimos. La clave está por tanto en saber dibujar en 2D. Los bocetos se crean desde el banco de trabajo part design
Explicación
Los bocetos los hacemos desde el banco de trabajo part design
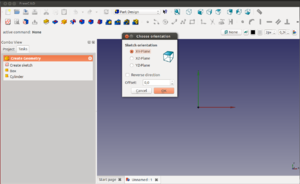
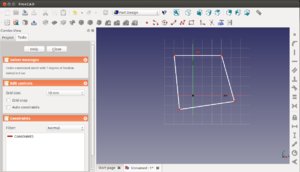
Para crear nuestro boceto "hola mundo", le damos al icono 
en la parte superior (o también a la opción create sketch con el mismo icono que se encuentra en la pestaña tasks). Aparecerá una ventana donde seleccionamos el plano en el que colocar el boceto. Lo situaremos en el suelo, en el plano xy (el que viene por defecto). Pinchamos en ok. Nos aparecerá un fondo cuadriculado.
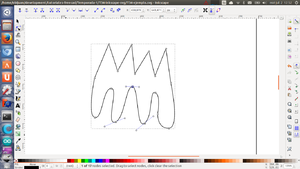
En la parte de la izquierda (en task) seleccionamos la opción "grip snap" y DESELECCIONAMOS la opción Auto-constraints (no queremos meter restricciones en este ejemplo). Vamos a dibujar una estrella a mano. No hace falta que quede perfecta, es un boceto :-) Pinchamos en el icono 
para hacer líneas múltiples. Comenzamos a dibujar la estrella. Cada vez que queramos finalizar una línea le damos al botón izquierdo. El último punto lo situamos encima del primero.
Una vez terminado, podemos mover cada punto dejando apretado el botón izquierdo del ratón y arrastrando el punto a la nueva posición. De esta forma podemos ajustar la forma de la estrella. Cuando hemos terminado de hacer el boceto le damos al botón de close. Por defecto veremos el boceto sobre el plano xy. Si le damos al icono de perspectiva isométrica lo veremos en 3D
Llega el momento de extruir el boceto para darle grosor y convertirlo en un objeto 3D. Seleccionamos el boceto y le damos al icono de extrusión (pad) 
. Por defecto se extruye una distancia de 10mm. La podemos cambiar o bien le damos al botón de OK para finalizar. ¡¡Ya tenemos nuestra estrella!!
Ahora tenemos 2 objetos: uno el boceto de la estrella (en 2D). Este boceto lo podemos trasladar y rotar. El otro es la estrella 3D generada mediante la extrusión lineal del boceto. Este objeto NO LO PODEMOS ni trasladar ni rotar, ya que depende del boceto. Esta relación de dependencia la podemos ver desde el menú tools/dependency graph. Cualquier cambio que hagamos en el bocetó hará que la estrella se modifique. Para editar el boceto hacemos doble click en él (en la ventana de la izquierda, en la pestaña de projects). Se nos abrirá el boceto (visto desde arriba) y nos aparecerá también la estrella 3D. Si queremos ver sólo el boceto, hacemos invisible la estrella, desde la pestaña proyecto (seleccionando la estrella y dándole al espacio).
Podemos editar también el boceto en perspectiva. Si pasamos a la perspectiva isométrica, veremos el boceto y encima la estrella 3D. Podemos mover los puntos de la estrella y veremos cómo la estrella 3D también cambia. Cuando finalizamos la edición le damos a Close. También podemos editar en todo momento la altura de la estrella. Para ella hacemos doble click en la estrella 3D (en la pestaña de proyectos). En el cuadro donde pone length podemos escribir la nueva altura (por ejemplo 40mm).
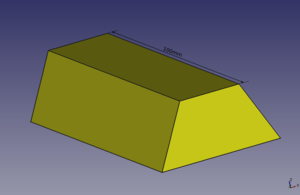
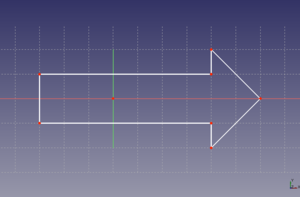
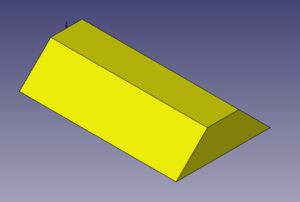
Ejercicios propuestos
- Ejercicio 1: Lingote de oro
- Ejercicio 2: Flecha
- Ejercicio 3: Rayo
- Entregas de Jose Ignacio Alonso @jialonso333 y Alfonso López
Ficheros
| T16-estrella.fcstd | Estrella (Freecad) |
| T16-estrella.stl | Estrella (STL) |
| T16-ej1-lingote.fcstd | Lingote (Freecad) |
| T16-ej1-lingote.stl | Lingote (STL) |
| T16-ej2-flecha.fcstd | Flecha (Freecad) |
| T16-ej2-flecha.stl | Flecha (STL) |
| T16-ej3-rayo.fcstd | Rayo (Freecad) |
| T16-ej3-rayo.stl | Rayo (STL) |
17 Extrusiones y vaciados
| Video Tutorial 17/40 |
|---|
Descripción
Los bocetos se puden extruir hacia afuera (pad), pero también hacia dentro (pocket) creando vaciados en las piezas
Explicación
Nos vamos a part design y creamos un boceto nuevo sobre el plano xy. Seleccionamos la poli-línea y hacemos un perímetro cerrado. Luego lo extruimos hacia fuera 20mm y lo renombramos como nivel-1
Ahora seleccionamos la superficie superior y le damos a crear un boceto. Este boceto quedará asociado a la superficie seleccionada. Hacemos otro perímetro cerrado usando la poli-línea.
El boceto está situado ahora encima del nivel 1. Lo extruimos 15mm
Seleccionamos la superficie superior del nivel 2 y creamos un nuevo boceto. Otra superficie cerrada
Este nuevo boceto lo vamos a usar para hacer un vaciado de 5mm de profundidad en el nivel 2. Para ello pulsamos en el icono pocket 
. Indicamos 5mm y le damos al ok. El vaciado aparece.
Hacemos otro vaciado que atraviese los dos niveles anteriores. Creamos un boceto nuevo al lado del vaciado anterior. Le damos al icono pocket y marcamos que sea de tipo through all. Luego creamos otro boceto al lado para hacer una torre de 50 mm (con pad)
Seleccionamos la cara frontal de la torre y creamos otro boceto en ella.
Hacemos que este boceto atraviese la torre por completo (pocket). Seleccionamos otra cara en el frontal del primer nivel
Y hacemos un último vaciado, que hace las veces de tunel. Ahora hacemos invisible todas las extrusiones y hacemos visibles los bocetos
Ejercicios propuestos
- Ejercicio 1: Robot calavera
- Ejercicio 2: Casa
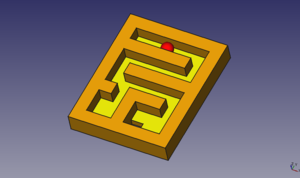
- Ejercicio 3: Juego del laberinto
- Entregas de JV Almodovar y Jose Ignacio Alonso (@jialonso333)
Ficheros
| T17-extrusion-vaciado.fcstd | Pieza del tutorial (Freecad) |
| T17-extrusion-vaciado.stl | Pieza del tutorial (STL) |
| T17-ej1-robot-calavera.fcstd | Robot calavera (Freecad) |
| T17-ej1-robot-calavera.stl | Robot calavera (STL) |
| T17-ej2-casa.fcstd | Casa (Freecad) |
| T17-ej2-casa.stl | Casa (STL) |
| T17-ej3-laberinto.fcstd | Laberinto (Freecad) |
| T17-ej3-laberinto.stl | Laberinto (STL) |
18 Aplicando restricciones
| Video Tutorial 18/40 |
|---|
Descripción
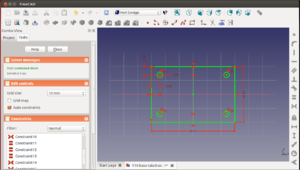
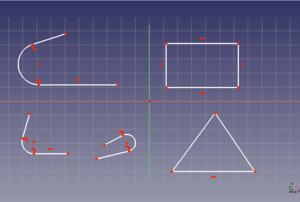
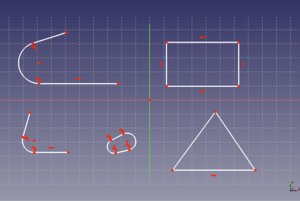
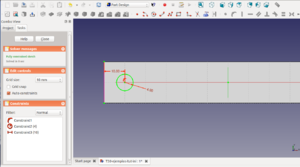
Los bocetos difieren del dibujo 2D tradicional. Con los bocetos se parte de algo genérico y poco a poco se va definiendo mediante la aplicación de restricciones. En este tutorial veremos las restricciones de puntos coincidentes, líneas horizontales, líneas verticales, misma longitud, cota horizontal y cota vertical.
Explicación
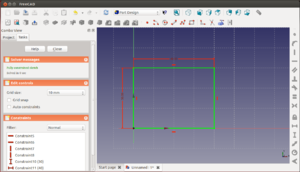
Creamos un boceto nuevo en el plano xy. Pinchamos en el icono de crear una línea 
y hacemos una línea. Repetimos la operación hasta que tengamos cuatro líneas independientes, como se muestra en la figura. Cada punto de las líneas lo podemos mover. Cada punto tiene 2 coordenadas, y como tenemos en total 8 puntos, nuestro boceto tiene 16 grados de libertad (hay que fijar 16 restricciones). Ahora seleccionamos 2 puntos, cada uno perteneciente a una línea. Lo hacemos haciendo click con el botón izquierdo. No hay que darle al ctrl. Cada vez que se selecciona uno se pone de color verde
Ahora le damos a la restricción de puntos coincidentes, representada mediante el icono 
. Los dos puntos se fusionarán en uno y las dos líneas quedarán unidas. Ahora hay 7 puntos, y el boceto tiene 14 grados de libertad pendientes de fijarse.
Si pinchamos en el nuevo punto y le damos a la tecla de suprimir, se elimina esta fución y vuelven a aparecer 2 puntos independientes.
Vamos a unir más puntos. Ahora lo haremos de otra manera. En vez de pinchar en cada punto, dejamos pinchado el botón izquierdo y creamos una caja de selección que contenga a los dos nuevos puntos a unir.
Aplicamos la restricción de puntos coincidentes y las líneas quedan unidas. Ahora tenemos 6 puntos y 12 grados de libertad. Hacemos lo mismo con el resto de puntos para que todas las líneas queden unidas. Estamos con 4 puntos y 8 grados de libertad.
Seleccionamos la arista superior. Se pondrá en verde. Vamos a aplicar una restricción de horizontalidad mediante el icono 
. Ahora la linea está simepre en posión horizontal, aunque se mueva la propia línea o los puntos de sus extremos. Los grados de libertad son 7
Hacemos lo mismo con la arista inferior. Ahora hay 6 grados de libertad. Seleccionamos las 2 aristas verticales (se pondrán en verde)
y aplicamos una restricción de verticalidad a ambas, pulsando el icono 
. Sólo quedan 4 grados de libertad.
A este mismo resultado se puede llegar de una manera más rápida. Una forma es haber usado la línea múltiple (icono ) activando la opción de auto-constraints (que viene por defecto). Con esta opción cuando se hacen líneas horizontales automáticamente se aplica la restricción de horizontalidad y lo mismo con la vertical. La otra forma es dibujando directamente un rectángulo con el icono 
. Sobre este rectángulo se aplican las restricciones de verticalidad y horizontalidad.
Las restricciones las eliminamos bien pinchando en la parte izquierda (donde están todas las restricciones) o bien marcando en los dibujos que hay al lado de las líneas (indicando el tipo de restricción). Una vez seleccionado le damos a la tecla de suprimir.
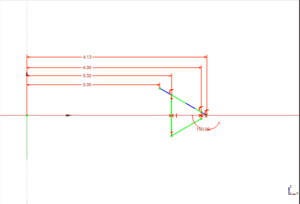
Marcamos la esquina inferior izquierda y el origen y aplicamos una restricción de coincidencia. El rectángulo se sitúa en el primer cuadrante. Sólo quedan 2 grados de libertad por fijar. Seleccionamos la arista vertical izquierda y pinchamos en el icono 
para fijar la cota vertical. Ahora sólo queda 1 grado de libertad
Si pinchamos en la cota, se nos habre un diálogo que nos permite especificar la distancia. Ponemos por ejemplo 30mm.
Ahora fijamos la cota horizontal con el icono 
. La ponemos a 40mm. El boceto pasa ahora a tener color verde. Esto significa que está totalmente definido. Si seleccionamos la cota horizontal y le damos a la tecla de suprimir, se elimina esta restricción. En ocasiones nos puede interesar hacer un cuadrado, en el que los dos lados son iguales. Para lograrlo usamos la restricción de igualdad. Seleccionamos dos líneas del cuadrado y pinchamos en el icono de igualdad: 
Ejercicios propuestos
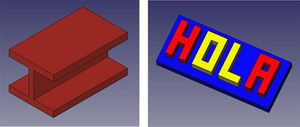
- Ejercicio 1: Viga en H
- Ejercicio 2: Letras
- Entregas de Alfonso López y Jose Ignacio Alonso
Ficheros
| T18-pieza-L.fcstd | Pieza en L (Freecad) |
| T18-pieza-en-L.stl | Pieza en L (STL) |
| T18-ej1-viga-H.fcstd | Viga en H (Freecad) |
| T18-viga-H.stl | Viga en H (STL) |
| T18-ej2-letras-HOLA.fcstd | HOLA (Freecad) |
| T18-HOLA.stl | HOLA (STL) |
19 Restricciones de simetría
| Video Tutorial 19/40 |
|---|
Descripción
Las restricciones de simetría nos permiten simplificar la creación de bocetos
Conceptos nuevo: Restricción de simetría, circunferencias, restricción de radio
Explicación
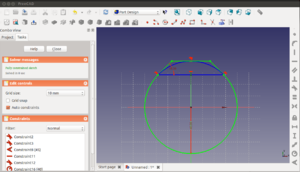
Vamos a utilizar la simetría para crear una base con 4 taladros. Creamos un boceto nuevo y hacemos un rectángulo inicial. A continuación seleccionamos los dos vértices superiores y el eje Y.
Aplicamos una restricción de simetría pinchando en el icono 
. Ahora, si movemos cualquier de los vertices superiores veremos cómo están siempre a la misma distancia del eje y. Ahora Seleccionamos los dos vértices de la izquierda y el eje X.
Le damos nuevamente al icono de restricción de simetría. Ahora al mover uno de los vértices automáticamente se moveran los otros 3 para cumplir con la restricción de simetría.
Vamos a colocar los taladros. Pinchamos en el icono 
y colocamos el primer taladro. No nos preocupamos por la posición ni por el diámetro.
Queremos que todos los taladros tengan el mismo diámetro. Los seleccionamos todos y pinchamos en el icono de restricción de igualdad
Ahora aplicamos las simetrías. Primero en los taladros superiores. Seleccionamos sus centros y el eje Y. Pinchamos en el botón de simetría. Repetimos la operación para los taladros inferiores. Por último lo hacemos en los dos taladros de la izquierda (o la derecha). Seleccionamos el eje x, sus centros y aplicamos la simetría. Ahora Al mover un taladro los otros 3 se moverán con él.
Si aplicamos la simetría del eje Y a los dos taladros de la derecha obtendremos un mensaje de error indicando que hay restricciones redundantes. Esto significa que hay demasiadas restricciones. Tenemos que eliminar la última.
Lo siguiente es fijar la posición de los taladros. Usaremos las cotas horizontales y verticales. Tomamos como referencia el taladro superior izquierdo (pero se puede tomar cualquiera de los otros). Pinchamos en el centro y en el vértice superior izquierdo. Aplicamos una restricción de cota horizontal. Le damos el valor de 6mm. Hacemos lo mismo pero con la cota vertical, con otro valor de 6mm. Si ahora movemos bien los taladros o bien los vértices vemos que cambian las dimensiones de la base, pero que todos los taladros permanencen a la misma distancia de los vértices.
Ahora fijamos el radio de los taladros. Pinchamos en el icono de fijar radio 
y damos un valor de 4mm
Quedan 2 grados de libertad por fijar: las dimensiones de la base. Usamos las cotas verticales y horizontales. Damos unas dimensiones de por ejemplo 60mm en el eje x, y 40 en el Y. El boceto se pondrá verde indicando que ya no quedan ningún grado de libertad adicional para fijar. Lo extruimos 4 mm y ya tenemos nuestra pieza.
Ejercicios propuestos
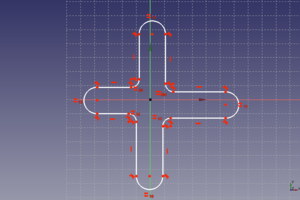
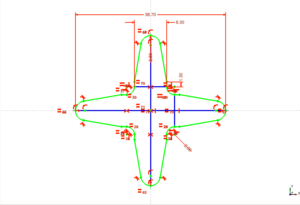
- Ejercicio 1: Ladrillo
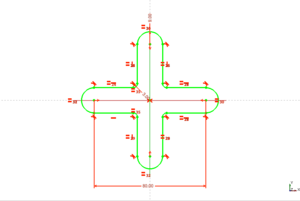
- Ejercicio 2: Pieza en cruz
- Ejercicio 3: Taburete
- Entregas de Jose Ignacio Alonso y Alfonso López
Ficheros
| T19-base-taladros.fcstd | Base con taladros (Freecad) |
| T19-base-taladros.stl | Base con taladros (STL) |
| T19-ej1-ladrillo.fcstd | Ladrillo (Freecad) |
| T19-ej1-ladrillo.stl | Ladrillo (STL) |
| T19-ej2-pieza-cruz.fcstd | Pieza en cruz (Freecad) |
| T19-ej2-pieza-cruz.stl | Pieza en cruz (STL) |
| T19-ej3-taburete.fcstd | Taburete (Freecad) |
| T19-ej3-taburete.stl | Taburete (STL) |
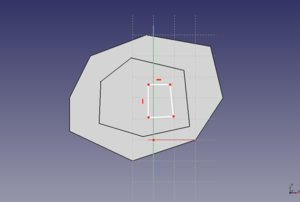
20 Bocetos de polígonos
| Video Tutorial 20/40 |
|---|
Descripción
Se muestra cómo fijar el ángulo entre dos líneas, para poder hacer figuras geométricas como triángulos y polígonos. También se introduce el concepto de línea auxiliar y de restricción de contacto.
- Conceptos nuevos: Restricción de contacto, líneas auxiliares y restricciones angulares
Explicación
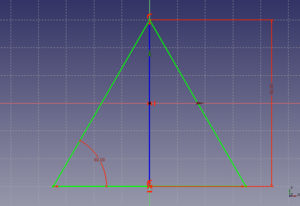
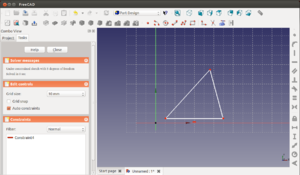
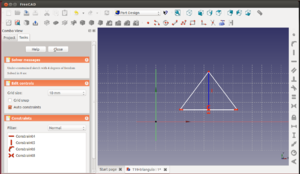
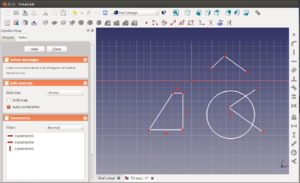
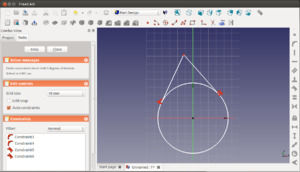
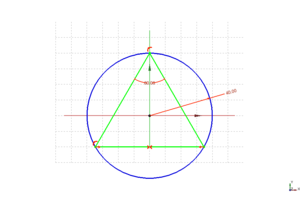
Empezamos haciendo un triángulo mediante la línea múltiple. Hacemos que la base del triángulo sea horizontal.
Ahora dibujarmos una línea vertical fuera del triángulo. La convertimos en una línea auxiliar seleccionándola y pinchando en el icono de línea auxiliar 
. Cambiará a color azul.
Vamos a hacer que el extremo inferior de la recta vertical se sitúe sobre la base del triángulo. Para ello seleccionamos la base y el punto
y pinchamos en el icono de restricción de contacto 
. El extremo se situará sobre la recta definida por la base del triángulo.
Hacemos que el extremo superior sea coincidente con el vértice superior del triángulo.Para convertir el triángulo en uno isósceles, definimos una restricción de simetría entre los dos extremos de la base y la altura.
Definimos otra restricción de simetría en la altura de manera que el eje x corte al triángulo por su parte media. Para que el origen se sitúe en el centro hacemos que los extremos de la altura sean simétricos con respecto al eje x.
Aplicaremos una restricción angular para determinar el ángulo entre la base y el lado izquierdo. Los seleccionamos y pulsamos el icono de fijar un ángulo 
. Ponemos por ejemplo un ángulo de 60 grados para que el triángulo sea equilátero.
Por último fijamos la altura a 60mm y extruimos una distancia de por ejemplo 100mm. Ya tenemos nuestro prisma de base triangular
Ejercicios propuestos
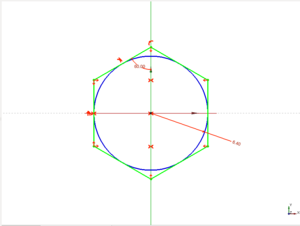
- Ejercicio 1: Hexágono regular
- Ejercicio 2: Pentágono regular
- Ejercicio 3: Estrella de 5 puntas
- Entregas de Roberto Carlos Carmona, Jose Ignacio Alonso y Jose del Valle
Ficheros
| T19-triangulo.fcstd | Prisma base triangular (Freecad) |
| T20-prisma-base-triangular.stl | Prisma base triangular (STL) |
| T19-ej1-hexagono.fcstd | Hexágono (Freecad) |
| T20-ej1-hexagono.stl | Hexágono (STL) |
| T20-ej2-pentagono.fcstd | Pentágono (Freecad) |
| T20-ej2-pentagono.stl | Pentágono (STL) |
| T20-ej3-estrella5.fcstd | Estrella de 5 puntas (Freecad) |
| T20-ej3-estrella.stl | Estrella de 5 puntas (STL) |
21 Arcos
| Video Tutorial 21/40 |
|---|
Descripción
Construcción de bocetos con arcos
- Conceptos nuevos: Arcos, restricción de tangencia, restricción de perpendicularidad
Explicación
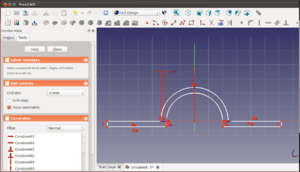
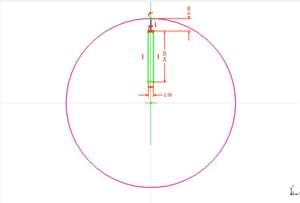
Creamos un boceto nuevo en el plano XZ. Colocamos un arco. Para ello pinchamos en el icono 
. Con el botón izquierdo posicionamos el centro del arco. Al hacerlo nos aparecerá una circunferencia blanca con el radio marcado. Colocamos el primer punto del arco pulsando el botón izquierdo del ratón. Ahora colocamos el siguiente punto y pulsamos nuevamente en el botón izquierdo. Nos aparecerá un arco, definido por 3 puntos: el centro y los extremos. Tendremos 5 grados de libertad.
Colocamos dos líneas horizontales coincidentes con los extremos del arco. Queremos que las líneas horizontales sean perpendiculares al arco en sus extremos. Para ello estableceremos una restricción de perpendicularidad. Seleccionamos una línea horizontal y el arco.
Ahora pulsamos en el icono de restricción perpendicular 
. Repetimos la operación con la línea horizontal de la derecha. Con ello conseguimos un arco que es una semicircunferencia (Arco de medio punto).
Creamos un arco nuevo. Hacemos que su centro sea coincidente con el arco anterior. Creamos dos líneas verticales y las hacemos coincidentes con los extremos del arco
Vamos a hacer que las líneas verticales sean tangentes al arco. Seleccionamos la línea vertical izquierda y el arco y aplicamos una restricción de tangencia pinchando en el icono 
.
Repetimos la misma operación con la otra línea vertical, para que también sea tangente al arco. Aplicamos además una restricción de igualdad para que tengan la misma longitud
Unimos las dos construcciones mediante poli-líneas, como se muestra en la figura. Ya se vislumbra la forma de la abrazacera. Aplicar restricciones de igualdad a las dos líneas inferiores de los laterales de la abrazadera
Quermeos que la abrazadera tenga el mismo espesor tanto en su base como en el arco. Para ello creamos una línea auxiliar en la parte inferior del arco. Aplicamos una restricción de igualdad para que su longitud sea igual a la anchura de la base.
Una vez que ya tenemos definida la forma de la abrazadera, vamos a empezar a definir su posición y dimensiones. Hacemos que el centro del arco coincida con el origen, mediante una restricción de coincidencia. Definimos el grosor aplicando una cota horizontal a la línea auxiliar antes creada. Ponemos por ejemplo 4mm
Fijamos el radio del arco interior, a por ejemplo 20mm. Por último fijamos la distancia de la parte izquierda de la base. El boceto cambia a color verde para indicarnos que está perfectamente definido.
Extruimos la abrazadera. Utilizamos la opción "Symmetric to plane" para que se extruya hacia ambos lados del plano zx (y quede centrada). Opcionalmente podemos ponerle taladros, bien usando cylindros que posicionamos y restamos, o bien creando un boceto en su base con los taladros y usando "pocket".
Ejercicios propuestos
- Ejercicio 1: Logo Opensource
- Ejercicio 2: Puente / acueducto
- Ejercicio 3: Gancho de ikea
- Entregas de Jose Ignacio Alonso y Roberto Carlos Carmona
Ficheros
| T21-abrazadera.fcstd | Abrazadera (Freecad) |
| T21-abrazadera.stl | Abrazadera (STL) |
| T21-ej1-logo-opensource.fcstd | Logotipo Opensource (Freecad) |
| T21-ej1-logo-opensource.stl | Logotipo Opensource (STL) |
| T21-ej2-puente.fcstd | Puente (Freecad) |
| T21-ej2-puente.stl | Puente (STL |
| T21-ej3-gancho-ikea.fcstd | Gancho ikea (Freecad) |
| T21-ej3-gancho-ikea.stl | Gancho Ikea (STL) |
22 ¡Qué vienen los recortes!
| Video Tutorial 22/40 |
|---|
Descripción
Se muestra cómo realizar recortes en líneas y curvas. Es una operación muy común, que se usa mucho con las líneas auxiliares de los bocetos
- Conceptos nuevos: Recorte
Explicación
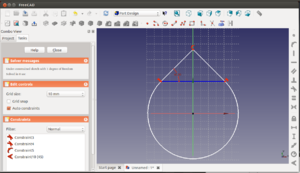
Partimos de un boceto inicial para hacer pruebas de recortes. Seleccionamos la herramienta de recorte pinchando en el icono 
. Situamos el cursor sobre el segmento a recortar.
Hacemos click con el botón izquierdo y el segmento se recorta hasta llegar a la intersección con la otra línea.
Ahora recortamos el rectángulo. Vamos pulsando en los segmentos que queremos eliminar hasta dejarlo como en la figura. Los círculos también se pueden recortar. Como ejemplo recortamos el sector del círculo
Como ejemplo de aplicación de los recortes, vamos a hacer un taladro de tipo reprap, que es como una gota de agua con la parte superior recortada. Comenzamos haciendo un círculo con centro en el origen y colocando dos líneas unidas, en la parte superior del círculo
Hacemos que los extremos de las líneas sean primero coincidentes con la circunferencia y después tangentes, usando la restricción de tangencia.
El punto superior lo hacemos coincidente con el eje Y. Ahora aplicamos la herramienta de recorte para eliminar el arco de circunferencia que hay entre los dos segmentos tangentes.
Los segmentos tiene que formar un ángulo de 45 grados al menos, para que al imprimirse el taladro el plástico no se descuelgue. Para ello hacemos una línea auxiliar que una los dos puntos de los extremos tangentes. Luego el ángulo entre el segmento izquierdo y la línea auxiliar de 45 grados. Con esto tenemos ya terminada la forma del taladro Reprap clásico.
Sin embargo, este taladro evolucionó y se comprobó que se podía reducir la altura total del taladro cortando la parte superior, sin perder calidad en su impresión. Tiramos un arco auxialiar entre los dos puntos de los extremos y colocamos una línea horizontal que sea tangente a este arco.
Recortamos las líneas superiores y los extremos sobrantes. El nuevo taladro está listo. Sólo falta especificar el radio del taladro. Lo fijamos por ejemplo a 40mm.
Finalmente lo extruimos y ¡ya tenemos nuestra pieza para hacer taladros en superficies verticales!
Ejercicios propuestos
- Ejercicio 1: Piezas con taladros reprap
- Ejercicio 2: Modelo de bote
- Ejercicio 3: Almenas de castillo
- Entregas de Jose Ignacio Alonso y Jose Raul Montero Ponce
Ficheros
| T22-reprap-drill.fcstd | Taladro reprap (Freecad) |
| T22-reprap-drill.stl | Taladro reprap (STL) |
| T22-ej1-reprap-drill2.fcstd | Pieza con 2 taladros reprap (Freecad) |
| T22-ej1-reprap-drill2.stl | Pieza con 2 taladros reprap (STL) |
| T22-ej2-bote.fcstd | Bote (Freecad) |
| T22-ej2-bote.stl | Bote (STL) |
| T22-ej3-almenas.fcstd | Almenas (Freecad) |
| T22-ej3-almenas.stl | Almenas (STL) |
23 Redondeando bocetos
| Video Tutorial 23/40 |
|---|
Descripción
Mediante líneas rectas, arcos y la restricción de tangencia se pueden hacer redondeos y refuerzos en bocetos. Sin embargo, se puede utilizar la herramienta de redondeo que te crea todo esto por ti, muy fácilmente
- Conceptos nuevos: herramienta de redondeo de bocetos
Explicación
Partimos de un boceto inicial sobre el que aplicaremos los redondeos. Primero pulsamos el icono de la herramienta de redondeo 
. Ahora seleccionamos los dos primeros segmentos, como se muestra en la figura.
Automáticamente aparecerá un arco unido a los dos segmentos y con las restricciones de tangencia y coincidencia creadas. Si movemos los nuevos puntos creados, veremos el arco y podremos cambiar los parámetros del redondeo. Para salir de la herramienta de redonde hay que hacer click con el botón izquierdo en cualquier parte del boceto donde no haya líneas ni puntos, o bien pulsar la tecla escape.
También se pueden unir mediante arcos segmentos que no están conectados entre sí. Se unirán por la parte donde el ángulo sea menor.
Para conseguir una forma cerrada mediante arcos, primero hay que mover los extremos a unir para que formen un ángulo menor de 90 grados y luego aplicar la herramienta de redondeo
También lo podemos aplicar para redondear las esquinas de un rectángulo. Primero seleccionamos las aristas del vértice inferior izquierdo. Luego repetimos para el resto de vértices.
Y para terminar con los ejemplos, hacemos lo mismo con un triángulo
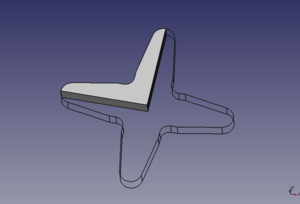
Como ejemplo de aplicación vamos a diseñar una pieza con 4 brazos, similares a las que se usan en los servos. Comenzamos haciendo un boceto. Como tiene 4 brazos, creamos una estrella con 4 brazos. Redondeamos los extremos de los brazos usando la herramienta de redondeo
Usamos restricciones verticales y horizontales en las aristas de los brazos. Mediante la restricción de igualdad, hacemos que todos los arcos de los extremos sean iguales.
Redondeamos los ángulos rectos interiores y aplicamos restricción de igualdad a los 4. También aplicamos las restricciones de igualdad a todos los lados de los brazos
Aplicamos simetrías en los centros de los arcos de los extremos, para que centrar la pieza en el origen. Finalmente damos valores a los radios exteriores: 9mm, a los interiores: 3mm y a la distancia entre centros: 80mm.
Ejercicios propuestos
- Ejercicio 1: Palanca de pinball
- Ejercicio 2: Pieza en L reforzada
- Ejercicio 3: Corona de 4 brazos para un servo Futaba 3003
- Entregas de Ruben Nieves López y Carlos Cervilla
Ficheros
| T23-ini.fcstd | Boceto inicial, de ejemplo para aprender a redondear (Freecad) |
| T23-pieza-cruz.fcstd] | Pieza con 4 brazos (Freecad) |
| T23-pieza-cruz.stl | Pieza con 4 brazos (STL) |
| T23-ej1-palanca-pinball.fcstd | Palanca de pinball (Freecad) |
| T23-ej1-palanca-pinball.stl | Palanca de pinball (STL) |
| T23-ej2-pieza-en-L.fcstd | Pieza en L (Freecad) |
| T23-ej2-pieza-en-L.stl | Pieza en L (STL) |
| T23-ej3-corona-futaba.fcstd | Corona de 4 brazos para servo Futaba 3003 (Freecad) |
| T23-ej3-corona-futaba.stl | Corona de 4 brazos para servo Futaba 3003 (STL) |
24 Restricciones externas
| Video Tutorial 24/40 |
|---|
Descripción
Cuando se crean piezas mediante bocetos, es necesario tener acceso a elementos externos al boceto para establecer restricciones con respecto a ellos, como por ejemplo partes coincidentes o cotas. Esto se consigue mediante la herramienta de acceso a elementos externos.
- Conceptos nuevos: Elementos externos
Explicación
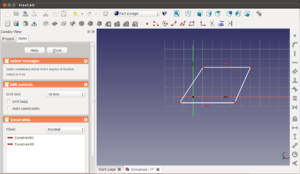
Comenzamos creando un boceto en el plano xy, con un rectángulo. Lo vamos a hacer simétrico con respecto al origen. Pinchamos en el punto de la esquina superior izquierda, luego en el de la esquina inferior derecha y finalmente en el origen. Aplicamos una restricción de simetría
El rectángulo queda simétrico con respecto a los ejes x,y. Ahora establecemos las dimensiones de las aristas horizontales y verticales a 50mm y 30mm respectivamente (por ejemplo)
Extruimos el boceto 10mm. Seleccionamos la cara superior
Creamos un boceto nuevo en la cara superior. Colocamos un rectángulo y lo hacemos que sea simétrico con respecto al eje y, para que quede centrado
Si ahora queremos hacer que este rectángulo se encuentre a una distancia fija de la arista superior de la pieza, tenemos que importar esa arista en nuestro boceto, y usarla de referencia para fijar restricciones. Eso lo hacemos pulsando el icono 
. A continuación seleccionamos la arista y pulsamos el botón izquierdo del ratón. Nos aparecerá una nueva arista en rosa, que es la proyección de la arista de la pieza en nuestro boceto.
Si hacemos no visible la pieza original, vemos nuestro boceto con la linea externa en rosa. Esta línea externa NO es una línea del boceto, sino que es similar a las líneas auxiliares. Si cerramos el boceto, la línea no la veremos.
Ahora ya podemos establecer la distancia entre la arista superior y nuestro rectángulo. Por último ponemos fijamos la anchura y altura del rectángulo
Ejercicios propuestos
- Ejercicio 1: Marco
- Ejercicio 2: Pieza con 4 alojamientos cuadrados
- Ejercicio 3: Escuadra reforzada
- Entregas de Jose Ignacio Alonso y JC Bedelber
Ficheros
| T24-pieza-ejemplo2.fcstd | Pieza de ejemplo (Freecad) |
| T24-pieza-ejemplo2.stl | Pieza de ejemplo (STL) |
| T24-ej1-marco.fcstd | Marco (Freecad) |
| T24-ej1-marco.stl | Marco (STL) |
| T24-ej2-pieza-alojamientos.fcstd | Pieza con alojamientos (Freecad) |
| T24-ej2-pieza-alojamientos.stl | Pieza con alojamientos (STL) |
| T24-ej3-escuadra-3D.fcstd | Escuadra reforzada (Freecad) |
| T24-ej3-escuadra.stl | Escuadra reforzada (STL) |
25 Extrusión axial
| Video Tutorial 25/40 |
|---|
Descripción
Generacion de sólidos de revolución mediante la extrusión axial. Se crea el perfil del objeto con un boceto, el cual se rota alrededor del eje vertical generando el sólido (o la superficie)
- Conceptos nuevos: Extrusión axial
Explicación
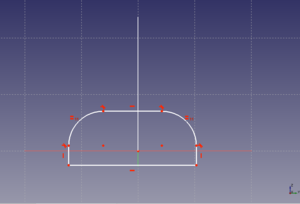
Creamos un boceto en el plano vertical xz, con el diseño mostrado en la figura, hecho con una línea múltiple. No hay que especificar las dimensiones. Cerramos el boceto
Para extruirlo axialmente seleccionamos el boceto y pulsamos el icono 
o le damos a la opción revolution en la pestaña de tasks (
).
Vamos a hacer ahora una rueda para el miniskybot. Comenzamos creando el boceto en el plano xz, con la forma mostrada en la figura. Luego establecemos las simetrías en el eje x
Ahora establecemos todas las cotas y ángulos para definir la rueda. La hendidura triangular (de 45 grados) es para colocar la junta tórica en la rueda. Se podría hacer con un semicírculo, sin embargo al hacerla triangular conseguimos que se imprima mejor (el plástico no se descuelga). Finalmente hacemos la extruxión axial para obtener la rueda
Ejercicios propuestos
- Ejercicio 1: Corona circular del servo Futaba 3003
- Ejercicio 2: Polea
- Ejercicio 3: Copa
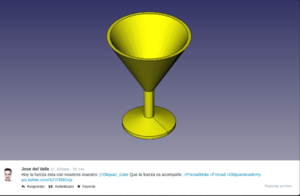
- Entregas de Jose del Valle y Jose Ignacio Alonso
Ficheros
| T25-rueda-miniskybot.fcstd | Rueda del miniskybot (Freecad) |
| T25-rueda-miniskybot.stl | Rueda del miniskybot (STL) |
| T25-ej1-corona-futaba3003.fcstd | Corona del servo Futaba 3003 (Freecad) |
| T25-ej1-corona-servo.stl | Corona del servo Futaba 3003 (STL) |
| T25-ej2-polea.fcstd | Polea (Freecad) |
| T25-ej2-polea.stl | Polea (STL) |
| T25-ej3-copa.fcstd | Copa (Freecad) |
| T25-ej3-copa.stl | Copa (STL) |
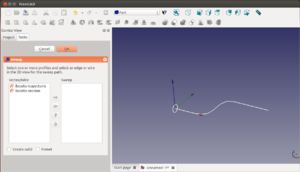
26 Extrusión por trayectoria
| Video Tutorial 26/40 |
|---|
Descripción
La extrusión no sólo se puede hacer lineal y axialmente, sino que también a lo largo de una trayectoria definida, lo que nos permite hacer fácilmente tuberías con curvas, railes, surcos, etc.
- Conceptos nuevos: Extrusión por trayectoria
Explicación
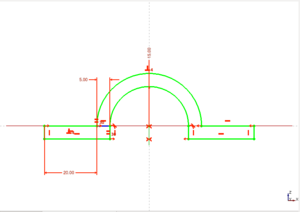
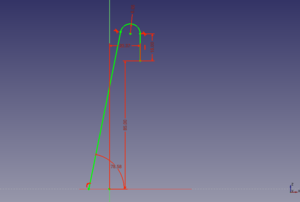
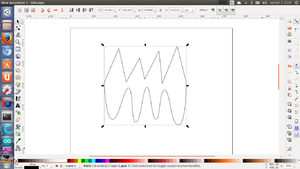
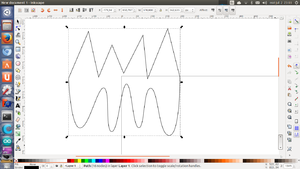
Comenzamos creando un boceto en blanco en el plano xz. Situamos 3 líneas, como en la figura, y luego las unimos mediante arcos con la herramienta de redondeo. Ya tenemos definida una trayectoria.
Ahora creamos otro boceto, pero en el plano yz. En este boceto definiremos la sección de nuestra pieza. Comenzaremos por una circunferencia, centrada en el origen. Cerramos el boceto. Lo vemos en perspectiva. Ahora tenemos una trayectoria y una sección. Renombramos los bocetos a boceto-trayectoria y boceto-sección para no confundirlos
Ahora nos vamos a banco de trabajo part y pinchamos en el icono sweep (barrido) 
. Se nos abrirá una nuevo menú en la pestaña de task. Seleccionamos la sección (boceto-seccion) y le damos al icono de la flecha que apunta a la derecha 
. Ahora seleccionamos en la ventana 3D todos los tramos de la trayectoria (dándole al control-botón izquierdo), hasta que quede en verde. También activamos la casilla "solid object"
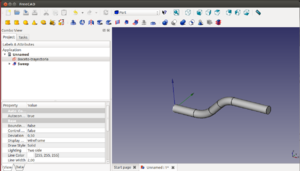
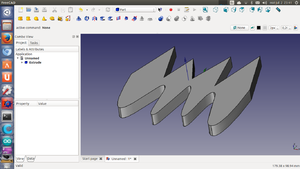
Le damos al bóton de ok y obtenemos nuestra figura:
Vamos a cambiar la sección de la pieza. Editamos el boceto de la sección. Borramos el círculo y ponemos un rectángulo centrado en el origen. Luego redondeamos los dos vértices superiores
Repetimos el proceso. Vamos al entorno part, pinchamos en el icono sweep, seleccionamos la nueva sección y le damos a la flecha, seleccionamos todos los tramos de la trayectoria, indicamos que queremos un objeto sólido y le damos al ok. Ya tenemos nuestra pieza.
Este es el resultado final (Usando la vista Shaded)
Ejercicios propuestos
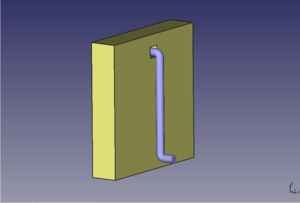
- Ejercicio 1: Gancho Ikea
- Ejercicio 2: Tubo en pared
- Ejercicio 3: Tobogán
- Entregas de Jose Ignacio Alonso y Jose Raul Montero Ponce
Ficheros
| T26-extrusion-path.fcstd | Ejemplo de extrusión por trayectoria (Freecad) |
| T26-extrusion-path.stl | Ejemplo de extrusión por trayectoria (STL) |
| T26-ej1-gancho-ikea.fcstd | Gancho de ikea (Freecad) |
| T26-ej1-gancho-ikea.stl | Gancho de ikea (STL) |
| T26-ej2-tuberia.fcstd | Tubería (Freecad) |
| T26-ej2-tuberia.stl | Tubería (STL) |
| T26-ej3-tobogan.fcstd | Tobogán (Freecad) |
| T26-ej3-tobogan.stl | Tobogán (STL) |
27 Interpolación de secciones
| Video Tutorial 27/40 |
|---|
Descripción
Mediante la interpolación de secciones se nos genera una pieza sólida a partir de dos o mas secciones
- Conceptos nuevos: Interpolación de secciones (Utilidad loft)
Explicación
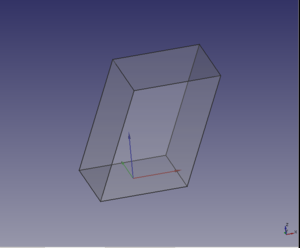
Partimos de un boceto de un cuadrado de 40mm de lado sobre el plano xy. Lo duplicamos (edit / duplicate selection) y lo desplazamos 50mm en z y 20mm en el eje Y
Renombramos los dos bocetos a boceto-base-inferior y boceto-base-superior. Vamos a usar esos dos bocetos para crear el sólido que los tiene como tapas superior e inferior. Nos vamos a entorno part y pinchamos en el icono loft 
. Se nos abrirá un menú en la pestaña task.
Seleccionamos el boceto inferior y le damos a la fecha azul que apunta a la derecha. Hacemos lo mismo con el boceto superior. Seleccionamos el cuadro que pone "Solid object". Al darle al ok nos aparecerá el nuevo objeto creado a partir de la interpolación de las dos secciones.
Ahora seleccionamos el boceto superior y lo rotamos 45 grados alrededor del eje z. Le damos al ok y nos aparecerá una nueva figura interpolada
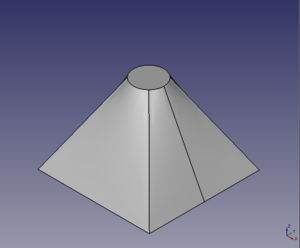
Vamos a hacer otro ejemplo. Partimos ahora de 2 bocetos cuadrados separados en z una distancia de 50mm. Esta vez están centrados, pero los cuadrados tienen distinto tamaño. Pinchamos en el icono de loft para crear la figura de interpolación. Seleccionamos el boceto de la base inferior y superior igual que hemos hecho antes. Marcamos que sea un objeto sólido. Y le damos al ok.
Aparecerá una pirámide truncada, de base cuadrada. Ahora editamos el boceto de la base superior y lo cambiamos por una circunferencia. Ahora se nos creará una nueva figura, en la que se partirá de una base cuadrada y termina en base superior circular.
Duplicamos la base inferior y la desplazamos 100mm en Z. Vamos a crear el nuevo objeto resultante de interpolar las 3 secciones. Usando la herramienta loft seleccionamos las 3 secciones y marcamos que sea un objeto sólido.
Le damos al ok y se nos general el objeto. Observamos que la unión entre las secciones se hace mediante curvas. Seleccionamos el nuevo objeto y nos vamos a sus propiedades en la pestaña DATA. Establecemos la propiedad "ruled" a true. Ahora nos aparecerá el objeto en el que se han unido las 3 secciones mediante rectas.
Ahora seleccionamos Solid igual a False. El objeto está ahora hueco por dentro (es una superficie). Finalmente ponemos Ruled también a false para ver la última variante
Ejercicios propuestos
- Ejercicio 1: Copa maciza
- Ejercicio 2: Volcan
- Ejercicio 3: Jarrón macizo
- Entregas de Jose Ignacio Alonso y Jose Raul Montero Ponce
Ficheros
| T27-tut1.fcstd | Paralelepípedo retorcido (Freecad) |
| T27-tut1.stl | Paralelepípedo retorcido (STL) |
| T27-tut1.fcstd | Segunda pieza de ejemplo (Freecad) |
| T27-tut2.stl | Segunda pieza de ejemplo (STL) |
| T27-ej1-copa.fcstd | Copa maciza (Freecad) |
| T27-ej1-copa.stl | Copa maciza (STL) |
| T27-ej2-volcan.fcstd | Volcán (Freecad) |
| T27-ej2-volcan.stl | Volcán (STL) |
| T27-ej3-jarron.fcstd | Jarrón macizo (Freecad) |
| T27-ej3-jarron.stl | Jarrón macizo (STL) |
28 Hélices y roscas
| Video Tutorial 28/40 |
|---|
Descripción
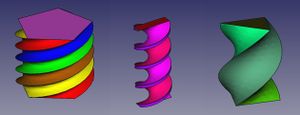
Las trayectorias en hélice se definen mediante cuatro parámetros: el paso, el radio, la altura y el ángulo de abertura. Con ellas, aplicando la extrusión por trayectoria, podemos crear hélices sólidas de diferentes secciones. Si la sección es circular, tendremos un muelle. Con las hélices podemos crear roscas macho y hembra, con las que podremos modelar cosas como tapones, tornillos y tuercas.
- Conceptos nuevos: Hélice, Rosca
Explicación
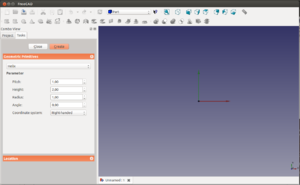
Partimos del banco de trabajo part y le damos al icono 
. Se nos abrirá un menú nuevo en la pestaña task. Allí vamos a la parte superior donde pone plane, pinchamos el desplegagle y seleccionamos helix. Nos aparecerá el menú para crear hélices, con sus 4 parámetros
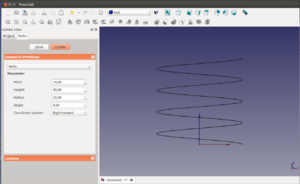
Vamos a crear una primera hélice que tenga 4mm de paso, 40mm de altura y 20mm de radio. El paso nos determina la distancia entre dos espiras consecutivas de la hélice. Ponemos los parámetros y le damos a Create. Nos aparece la hélice. Le damos al icono de vista en perspectiva. El menú de la hélice no ha desaparecido. Está todavía abierto para crear más hélices.
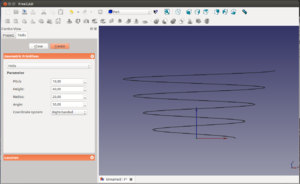
Seleccionamos la hélice en la vista 3D y la borramos (con la tecla supr.). Vamos a crear otra hélice que tenga los mismos parámetros que la anterior pero con 10mm de paso. Ahora la distancia entre espiras es mayor. La borramos y creamos otra nueva, modificando el ángulo para que en vez de 0 sea de 30 grados. Lo que ocurre ahora es que la hélice se va abriendo. Los extremos están inclinados un ángulo de 30 grados.
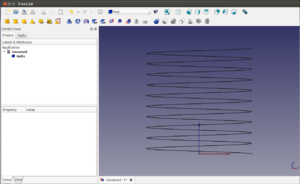
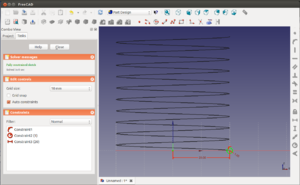
Para los siguientes objetos nos quedamos con la hélice original (4mm de paso, 40mm de altura, 20 de radio y 0 grados). Creamos un boceto en el plano xz que tenga una circunferencia de radio = 1mm situada en el eje x, a una distancia de 20mm del origen
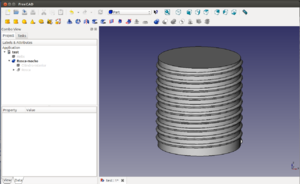
Ahora aplicamos una extrusión por trayectorias a la sección circular. Seleccionamos la sección, la hélice en la vista 3D, y marcamos las casillas que de objeto sólido y FRENET. Al darle al ok, nos aparecerá la rosca de sección circular. Es en realidad igual que un muelle. Esta operación puede tardar tiempo, dependiendo del ordenador que tengamos.
Creamos un cilindro de 20mm de diámetro y 44mm de altura. Lo desplazamos 2mm en el eje z para centrarlo y lo unimos a la rosca. Obtenemos una rosca macho.
Ahora hacemos un tapón roscado. Creamos un cilincro de 24mm de radio y 30mm de altura. Desplazamos la rosca hasta la posición z = 5, de manera que el tapón tenga 3mm de grosor en la parte superior
Restamos la rosca al cuerpo del tapón. Ya tenemos nuestro tapón listo. Finalmente le cambiamos el color y visualizamos la rosca macho
Ejercicios propuestos
- Ejercicio 1: Amortiguador
- Ejercicio 2: Tornillo M8
- Ejercicio 3: Tuerca M8
Algunas directrices para explicar cómo hay que hacer la tuerca. Se parte de un cuerpo hexagonal definido por el boceto anterior. Sobre él hay que hacer un taladro de 6.8mm de diámetro. A continuación se hace un chaflán en la parte interior, tanto en la superior como inferior, de 1mm de radio.
Ahora hacemos un chaflán externo. Para ello creamos el boceto mostrado en la figura y lo extruimos axialmente
Para hacer el chaflán externo restamos la pieza a la tuerca. Finalmente restamos la rosca también a la tuerca, con lo que obtenemos el roscado interior
- Entregas de Jose Ignacio Alonso y Ruben Nieves
Ficheros
| T28-helice-rosca-tapon.fcstd | Tapón roscado y rosca macho (Freecad) |
| T28-rosca-macho.stl | rosca macho (STL) |
| T28-rosca-tapon.stl | Tapón roscado (STL) |
| T28-ej1-amortiguador.fcstd | Amortiguador (Freecad) |
| T28-ej1-amortiguador.stl | Amortiguador (STL) |
| T28-ej2-tornillo-M8.fcstd | Tornillo M8 (Freecad) |
| T28-ej2-tornillo.stl | Tornillo M8 (STL) |
| T28-ej3-tuerca-M8.fcstd | Tuerca M8 (Freecad) |
| T28-ej3-tuerca-M8.stl | Tuerca M8 (STL) |
29: Extrusión con torsión
| Video Tutorial 29/40 |
|---|
Descripción
Los bocetos se pueden extruir verticalmente con torsión, de manera que roten a medida que se extruyen. La manera de hacerlo es utilizando una hélice, un boceto en el plano xy y una extrusión por trayectorias. Para establecer el ángulo de torsión que queramos, calculamos el paso mediante la siguiente fórmula: P = 360 * H / angulo, donde H es la altura y ángulo el ángulo de torsión en grados.
- Conceptos nuevos: Extrusión con torsión, vista de torno, consola de python
Explicación
Vamos a crear un prisma de base cuadrada al que le aplicaremos una torsión. Primero creamos el boceto de la base del prisma: un cuadrado centrado en el origen de 3mm de lado. Luego creamos una hélice de paso 50mm, algura 50mm y el radio es indiferente. Le damos por ejemplo un radio de 10mm
Le damos a create y nos aparecerá la hélice en negro. Ahora vamos a realizar una extrusión por trayectoria usando esa hélice. Le damos al icono de extrusión por trayectoria, seleccionamos el boceto, seleccionamos la hélice en la vista 3D y pinchamos en las casillas de solid y Frenet.
Le damos al ok y se nos extruye el cuadrado con torsión. Como la hélice tiene un paso de 50mm (igual a la altura) significa que la base se rotará un ángulo de 360 grados. En la imagine parece que ha rotado más. Sin embargo, si seleccionamos una de las hélices laterales, comprobamos que efectivamente el cuadrado ha rotado 360 grados.
Si miramos el diagrama de dependencias (Tools/dependency graph) vemos que el prisma extruido con torsión depende del boceto y de la hélice. Esto significa que si modificamos los parámetros de la hélice, automáticamente se modificará el prisma. Vamos a cambiar el ángulo de torsión a 90 grados. El paso que tenemos que aplicar se calcula mediante la fórmula: P = 360 * H / ángulo_torsión. Vamos a hacer el cálculo en la consola de python de Freecad. Para abrirla le damos a la opción del menú: view/views/python console
En la consola escribimos directamente el cálculo a hacer: 360 * 50 / 90, donde 50 es la altura del prisma y 90 el ángulo (en grados) de la torsión. Como resultado nos saldrá un valor del paso de 200. Lo modificamos en la hélice y automáticamente nos aparecerá el nuevo prisma.
Vamos a jugar con la torsión. Aplicamos un ángulo de 45 grados (usando la fórmula anterior sale un paso de 400mm). Luego modificamos la altura a 100mm
Vamos a decorar un poco las hélices. En total hay 4, una para cada lado del cuadrado. Seleccionamos el prisma y le damos al botón derecho y pinchamos en "set colors". Seleccionamos la primera helice y le asignamos el color amarillo. Repetimos con el resto de hélices y les damos los colores amarillo, rojo, naranja y verde.
Vamos a hacer que la pieza rote automáticamente. Activamos la vista frontal y le damos a Tools/view turntable. Se nos abrirá una nueva ventana donde podemos controlar el ángulo de la pieza y la velocidad de rotación. Le damos al Play para que empiece a moverse.
Ejercicios propuestos
- Ejercicio 1: Prisma triangular con torsión. Altura 100mm. Ángulo de torsión: 120 grados
- Ejercicio 2: Prisma rectangular con torsión. Altura 100mm. Ángulo de torsión: 360 x 2 grados (2 vueltas)
- Ejercicio 3: Prisma pentagonal con torsión. Altura 50mm. Ángulo de torsión: 360 grados
- Entregas de Jose Ignacio Alonso y Rubén Nieves
Ficheros
| T29-prisma-cuadrado-torsion.fcstd | Prisma de base cuadrada, con torsión (Freecad) |
| T29-prisma-cuadrado-torsion-1.stl | Prisma de base cuadrada, con torsión. 360 grados. Altura: 50mm (STL) |
| T29-prisma-cuadrado-torsion-2.stl | Prisma de base cuadrada, con torsión. 90 grados. Altura: 50mm (STL) |
| T29-prisma-cuadrado-torsion-3.stl | Prisma de base cuadrada, con torsión. 45 grados. Altura: 50mm (STL) |
| T29-prisma-cuadrado-torsion-4.stl | Prisma de base cuadrada, con torsión. 90 grados. Altura: 100mm (STL) |
| T29-ej1-prisma-triangular-torsion.fcstd | Prisma triangular con torsion (Freecad) |
| T29-ej1-prisma-triangular-torsion.stl | Prisma triangular con torsion (STL) |
| T29-ej2-prisma-rectangular-torsion.fcstd | Prisma rectangular con torsión (Freecad) |
| T29-ej2-prisma-rectangular-torsion.stl | Prisma rectangular con torsión (STL) |
| T29-ej3-prisma-pentagonal-torsion.fcstd | Prisma pentagonal con torsión (Freecad) |
| T29-ej3-prisma-pentagonal-torsion.stl | Prisma pentagonal con torsión (STL) |
30 Repeticiones y bocetos
| Video Tutorial 30/40 |
|---|
Descripción
Además de aplicar repeticiones sobre objetos, también es posible aplicar repeticiones a bocetos hechos sobre las piezas, permitiendo hacer repeticionces de taladros, vaciados y salientes
- Conceptos nuevos: Repetición de bocetos lineal y polar. Grupos
Explicación
Partimos de tres piezas base, sobre las que aplicaremos las repeticiones. Cada pieza está metida en una carpeta diferente en el árbol de objetos. Esta es una manera de organizar los objetos cuando se tienen varios. Comenzamos con la pieza 1. Hacemos invisibles el resto
Seleccionamos la parte superior de la pieza 1 y creamos un boceto nuevo. Colocamos un taladro de 4mm sobre el eje x, a una distancia de 10mm del borde izquierdo.
Cerramos el boceto y extruimos el agujero hacia el interior una distancia de 5mm. Ahora seleccionamos la pieza y pinchamos en el icono 
. Se nos abrirá un menú nuevo en la pestaña task de la izquierda. Incrementamos el número de repeticiones (ocurrencies).
Fijamos el número a 8 y le damos al ok. Ya tenemos la pieza 1 lista
Ahora hacemos visible la pieza 2. Sobre ella colocamos el boceto mostrado en la figura
Lo extruimos 10mm y lo repetimos igual que antes. Seleccionamos el objeto extruido y pinchamos en el icono y se nos abre el menú. Le decimos que la distancia total sea de 60mm y las ocurrencias de 6. Le damos al ok.
Hacemos visible la pieza 3 y sobre ella colocamos el boceto de un taladro
Lo extruimos hacia dentro (pocket) para obtener el taladro. Seleccionamos la pieza y pinchamos en el icono 
, para realizar una repetición axial. Se abriŕa un menú en la pestaña task.
Por defecto está puesto un ángulo de 360 grados. Incrementamos el número de taladros hasta llegar a 10. Podemos modificar el ángulo para que estos taladros se repartan a lo largo de un ángulo diferente de 360 grados. Para terminar le damos al ok.
Ejercicios propuestos
- Ejercicio 1: Peine
- Ejercicio 2: Pieza de Lego
- Ejercicio 3: Porta SDs circular
- Entregas de Jose Ignacio Alonso y Bedelber, J.C
Ficheros
| T30-ejemplos-tut-ini.fcstd | Piezas Iniciales, sobre las que se aplican las repeticiones en el tutorial (Freecad) |
| T30-ejemplos-tut.fcstd | Ejemplos mostrados en el tutorial (Freecad) |
| T30-ejemplo-pieza-1.stl | Pieza de ejemplo 1 (STL) |
| T30-ejemplo-pieza-2.stl | Pieza de ejemplo 2 (STL) |
| T30-ejemplo-pieza-3.stl | Pieza de ejemplo 3 (STL) |
| T30-ej1-peine.fcstd | Peine (Freecad) |
| T30-ej1-peine.stl | Peine (STL) |
| T30-ej2-pieza-lego.fcstd | Pieza Lego (Freecad) |
| T30-ej2-pieza-lego.stl | Pieza Lego (STL) |
| T30-ej3-portasds.fcstd | Porta SDs circular (Freecad) |
| T30-ej3-porta-sd.stl | Porta SDs circular (STL) |
31 Simetría de espejo: espejito, espejito
| Video Tutorial 31/40 |
|---|
Descripción
Muchas piezas tienen simetría de espejo. Esto nos permite sólo diseñar una parte de esta pieza, obteniendo el resto aplicando la simetría de espejo, lo que nos ahorra muchísimas trabajo. Podemos aplicar esta simetría tanto a piezas como a bocetos extruidos (vaciados, taladros y salientes)
- Conceptos nuevos: Simetría de espejo en piezas, simetría de espejo en bocetos
Explicación
Partimos de "un cuarto" de una pieza. Se corresponde con el cuarto superior izquierdo de una pieza más grande. Nos vamos al banco de trabajo part. Seleccionamos la pieza y pinchamos en el icono 
para aplicar la simetría de espejo. Se abre un menú en la parte izquierda. Ahí seleccionamos como plano de simetría el YZ.
Le damos al ok y nos aparece la misma pieza pero con la simetría de espejo aplicada sobre el plano YZ. Ahora seleccionamos ambas piezas y las fusionamos mediante una unión. Ya tenemos la mitad de la pieza final.
Seleccionamos la nueva pieza y volver a dar al icono de simetría de espejo . Esta vez seleccionamos el plano XZ y le damos al ok. Ahora tenemos la mitad superior e inferior de la pieza 1
Por último seleccionamos las dos mitades y las fusionamos.
Ahora vamos a modificar el boceto original, cambiando sus dimensiones. Al cerrarlo, automáticamente se nos actualizará la pieza completa, aplicándose las simetrías de espejo y uniones correspondientes
Hacemos invisible la pieza 1 y mostramos la base de la pieza 2. Nos vamos al banco de trabajo part design. Seleccionamos la parte superior y colocamos un boceto de un triángulo para hacer un vaciado.
Le damos a pocket para hacer el primer vaciado. Seleccionamos la pieza y pinchamos en el icono 
. Automáticamente aparece un vaciado simétrico
Finalmente modificamos el boceto. Le damos a close y vemos cómo nos cambian los dos vaciados: el original y el que tiene la simetría.
Ejercicios propuestos
- Ejercicio 1: Smiley reloaded!
- Ejercicio 2: Corona del servo reloaded!
- Ejercicio 3: Perfil de aluminio
- Entregas de Jose Ignacio Alonso y Bedelber JC
Créditos
- El diseño original del perfil de aluminio está sacado de la biblioteca libre BOLTS. Yo lo he modificado para construirlo con simetrías de espejo
Ficheros
| T31-mirror-ini.fcstd | Piezas iniciales, sobre las que se hacen los ejemplos del tutoria 31 (Freecad) |
| T31-mirror.fcstd | Ejemplos mostrados en el tutorial (Freecad) |
| T31-mirror-pieza-1.stl | Pieza de ejemplo 1 (STL) |
| T31-mirror-pieza-2.stl | Pieza de ejemplo 2 (STL) |
| T31-ej1-smiley.fcstd | Smiley reloaded! (Freecad) |
| T31-ej1-smiley.stl | Smiley reloaded! (STL) |
| T31-ej2-corona-futaba.fcstd | Corona para servo futaba 3003 (Freecad) |
| T31-ej2-corona-futaba.stl | Corona para servo Futaba 3003 (STL) |
| T31-ej3-perfil.fcstd | Perfil de aluminio, 20mm (Freecad) |
| T31-ej3-perfil-aluminio.stl | Perfil de aluminio, 20mm (STL) |
32 Herramienta de Offset
| Video Tutorial 32/40 |
|---|
Descripción
Mediante la herramienta de offset hacemos que las piezas crezcan una distancia por cada una de sus caras. La nueva pieza puede tener unidas sus caras mediante redondeos. De esta forma podemos redondear piezas con muchas aristas, sin tener que estar seleccionándolas. Además, cuando se hacen piezas en las que haya otras piezas que las atraviese (como en el caso de guías, tuercas empotradas, alojamientos, etc) hay que dejar una holgura. Esto se consigue aplicando un offset y luego haciendo la diferencia. El nuevo vaciado tendrá la holgura que le hayamos dado con el offset.
- Conceptos nuevos: Herramienta de offset
Explicación
Partimos de una pieza creada a partir de la extrusión de un boceto. Desde el banco de trabajo part, seleccionamos la pieza y pinchamos en el icono de aplicar el offset 
. Aparecerá una nueva pieza que recubre a la original, cuyos lados están a una distancia de 1mm de los originales. La unión entre las caras agrandadas se hace aplicando redondeos por defecto.
Le damos al ok. Hacemos transparente la pieza con offset y cambiamos el color de la pieza original a amarillo para apreciar mejor este efecto offset. Hacemos sobre una esquina. Podemos apreciar mejor el offset y la unión redondeada.
Hacemos doble click en la pieza con offset (en la parte del proyecto) para que se abra de nuevo el menú de offset. Cambiamos el tipo de union (Join type) a Intersection. El objeto con offset ahora ya no acaba con redondeos. Vamos a usar este modo para crear un vaciado en otra pieza, de manera que la pieza original tenga una tolerancia y pueda pasar a través de este vaciado.
Seleccionamos la pieza base, la pieza con offset y hacemos la diferencia. Ahora podemos ver cómo la pieza original atraviesa el nuevo agujero, pero no toca las paredes. Hay una holgura. Esto se ve mejor desde la vista superior. La holgura se ha dejado de 1mm (valor dado al offset). Es una holgura muy grande. Se ha usado esta para que se vea mejor en el tutorial. Sin embargo, se puede editar este offset y cambiarlo a 0.2mm. Automáticamente se recalculará todo.
Ejercicios propuestos
- Ejercicio 1: Pieza con 2 tuercas M3 empotradas
- Ejercicio 2: Rueda con corona de servo
- Ejercicio 3: Juego de piezas
- Entregas de Jose Ignacio Alonso y Ruben Nieves López
Ficheros
| T32-ejemplo-ini.fcstd | Ejemplo inicial, con las piezas para comenzar el tutorial (Freecad) |
| T32-ejemplo.fcstd | Ejemplo del tutorial, terminado (Freecad) |
| T32-ejemplo-base.stl | Pieza base del ejemplo (STL) |
| T32-ejemplo-macho.stl | Pieza macho, del ejemplo (STL) |
| T32-ej1-tuerca-empotrada.fcstd | Ejercicio 1: pieza con tuercas empotradas (Freecad) |
| T32-ej1-tuerca-empotrada.stl | Ejercicio 1: pieza con tuercas empotradas (STL) |
| T32-ej2-rueda-miniskybot.fcstd | Ejercicio 2: Rueda del miniskybot con hueco para la corona del servo (Freecad) |
| T32-ej2-rueda-miniskybot.stl | Ejercicio 2: Rueda del miniskybot con hueco para la corona del servo (STL) |
| T32-ej3-juego-piezas.fcstd | Ejercicio 3: Juego de piezas (Freecad) |
| T32-ej3-juego-piezas.stl | Ejercicio 3: Juego de piezas (STL) |
33 Thickness: Haciendo recipientes
| Video Tutorial 33/40 |
|---|
Descripción
Para hacer recipientes usamos la herramienta thickness en el banco de trabajo part. Hay que hacer el recipiente como un objeto sólido, seleccionar la cara por donde queremos hacer el vaciado y usar la herramienta thickness para vaciarla, estableciendo el grosor que queremos para las paredes.
- Conceptos nuevos: Herramienta thickness
Explicación
Partimos de una caja inicial que queremos convertir en un recipiente. Como es un objeto sencillo, una forma sería restando otra caja situada en el interior. Sin embargo, lo podemos hacer más fácil usando la herramienta thickness. Seleccionamos la parte superior de la caja y desde el banco de trabajo part pinchamos en el icono thickness 
. Se nos abre un menú nuevo y se nos vacía la caja.
Por defecto las paredes tienen un grosor de 1mm. La parte exterior ha crecido (igual que con la herramienta de offset) y podemos hacer que sea redondeada o picuda. Cambiamos el tipo de unión a intersection. Ahora el exterior tiene bordes afilados (a 90 grados). También podemos determinar el grosor de las paredes del recipiente. Lo cambiamos a 4mm.
El grosor de las paredes se puede poner negativo. En ese caso crecen hacia la parte interior. Por ejemplo, vamos a ponerlas a -3mm. Para terminar este recipiente dejamos el grosor a 2mm, con redondeos, cambiamos el color a azul y lo hacemos transparente para ver el interior
Mostramos la siguiente figura: un cilindro. Vamos a convertirlo en recipiente. Repetimos el proceso. Seleccionamos la tapa superior y pinchamos en el icono de thickness. Seleccionamos tipo de unión intersección
Le damos al ok. Cambiamos el color a violeta. Visualizamos el próximo objeto: una esfera. Modificamos sus propiedades poniendo el ángulo 1 a -40 y el ángulo 2 a 70, para que tenga tanto la parte superior como la inferior planas
Seleccionamos la tapa superior y le damos al icono de thickness. Dejamos el grosor a 1mm y ponemos el tipo de unión a intersection
Ponemos el recipiente de color amarillo. Por último visualizamos el cuarto objeto: un prisma de base cuadrada al que se le ha aplicado una torsión. Lo convertimos en recipiente de la misma manera: seleccionamos la tapa superior y pinchamos en thickness. Establecemos un grosor de 2mm y una intersección de tipo arco. Le damos al ok y le cambiamos el color a verde.
No todas las figuras las podremos convertir a recipientes. Algunas figuras complejas nos pueden dar problemas y freecad se quedará colgado. En las siguientes versiones se irá mejorando esta herramienta.
Ejercicios propuestos
- Ejercicio 1: Convertir en recipiente el prisma pentagonal con torsión del ejercicio 3 del tutorial 29
- Ejercicio 2: Copa
- Ejercicio 3: Jarrón
- Entregas de Jose Ignacio Alonso y Ruben Nieves López
Ficheros
| T33-ejemplo-ini.fcstd | Piezas de ejemplo iniciales, para hacer el tutorial (Freecad) |
| T33-ejemplo.fcstd | Piezas de ejemplo mostradas en el tutorial (Freecad) |
| T33-recipiente-base-cuadrada.stl | Recipiente de base cuadrada (STL) |
| T33-recipiente-cilindrico.stl | Recipiente cilíndrico (STL) |
| T33-recipiente-esferico.stl | Recipiente esférico (STL) |
| T33-recipiente-base-cuadrada-torsion.stl | Recipiente cuadrado con torsión (STL |
| T33-ej1-recipiente-prisma-pentagonal-torsion.fcstd | Ejercicio 1. Recipiente: prisma pentagonal con torsión (Freecad) |
| T33-ej1-recipiente-prisma-pentagonal-torsion.stl | Ejercicio 1. Recipiente: prisma pentagonal con torsión (STL) |
| T33-ej2-vaso.fcstd | Ejercicio 2. Vaso (Freecad) |
| T33-ej2-vaso.stl | Ejercicio 2. Vaso (STL) |
| T33-ej3-jarron.fcstd | Ejercicio 3. Jarrón (Freecad) |
| T33-ej3-jarron.stl | Ejercicio 3. Jarrón (STL) |
Trabajando con otros formatos y aplicaciones externas
34 Programa Inkscape: importando ficheros SVG en Freecad
| Video Tutorial 34/40 |
|---|
Descripción
El inkscape es un programa libre y multiplataforma (es parte del patrimonio tecnológico de la humanidad) para hacer dibujos no técnicos en 2D. Usando inkscape podemos hacer o editar dibujos 2D, exportarlos a formato SVG plano, importarlos en Freecad y extruirlos. De esta forma podemos incorporar a nuestros diseños partes artísticas que no serían fácil de hacer directamente con Freecad.
- Conceptos nuevos: Dibujo de líneas y curvas de bezier en inkscape. Exportando a svg plano. Importando svgs desde freecad. Extrusión de trayectorias
Explicación
Una vez instalado el inkscape, lo abrimos. Manteniendo apretada la tecla ctrl y dándole a la rueda del ratón hacemos zoom hacia dentro y hacia fuera. Si mantenemos pulsada la tecla ctrl y pulsamos el botón central del raton, nos desplazamos horizontal y verticalmente.
Haremos un garabato formado por rectas y curvas. Pinchamos en el icono 
. Cada vez que hagamos click en el botón izquierdo del ratón se comienza a dibujar una recta. Dibujamos unas cuantas rectas, como se muestra en la figura. A continuación vamos a empezar a hacer curvas de Bezier. Dejando pulsado el botón izquierdo del ratón, lo arrastramos y aparecen los tiradores del punto. Soltamos el botón izquierdo. Hemos hecho la primera curva
Ahora hacemos una segunda curva. Pinchamos otra vez en el botón izquierdo, lo arrastramos, salen los tiradores y soltamos el botón. Repetimos hasta terminar todas las curvas. Situamos el último punto sobre el primero y le damos al botón izquierdo.
El garabato está terminado. Ahora lo editamos. Pinchamos en el icono 
. Aparecen todos los puntos. Los podemos recolocar. En el caso de los puntos de las curvas de bezier, al pinchar sobre ellos aparecen los tiradores que nos permite ajustar el radio de curvatura y la orientación
Una vez editado, salimos del modo edición dándole al icono 
. Movemos el dibujo a la esquina superior izquierda, que es donde está el origen de Freecad. Ahora lo grabamos. Le damos al menú file/save as...
Seleccionamos el formato Plain SVG, le damos un nombre al fichero (por ejemplo t.svg) y pinchamos en save
Abrimos el freecad. Seleccionamos el banco de trabajo part. Vamos a la opción file/import. Seleccionamos el fichero t.svg y le damos a open.
Se nos abre una ventana con dos opciones. Seleccionamos "SVG as geometry (import SVG)" y pinchamos en Select.
El dibujo está situado sobre el plano xy. Seleccionamos el dibujo y pinchamos en el icono 
. Se nos abrirá un menú en la parte izquierda. Marcamos "Create Solid" y ponemos 10mm en la longitud.
Le damos al botón de apply y se extruye el dibujo
Ejercicios propuestos
- Ejercicio 1: Bocadillo de comic
- Ejercicio 2: Ondulaciones
- Ejercicio 3: Monigote
- Entregas de Jose Ignacio Alonso y xxx
| [[|thumb|300px| (click para ampliar)]] | [[|thumb|300px| (click para ampliar)]] |
Ficheros
| T34-ejemplo.fcstd | Garabato de ejemplo (Freecad) |
| T34-ejemplo.svg | Garabato de ejemplo (SVG, inkscape) |
| T34-ejemplo.stl | Garabado de ejemplo (STL) |
| T34-ej1-bocadillo-comic.fcstd | Ejercicio 1: Bocadillo (Freecad) |
| T34-ej1-bocadillo-comic.svg | Ejercicio 1: Bocadillo (SVG, Inkscape) |
| T34-ej1-bocadillo.stl | Ejercicio 1: Bocadillo (STL) |
| T34-ej2-ondulaciones.fcstd | Ejercicio 2: Ondulaciones (Freecad) |
| T34-ej2-ondulaciones.svg | Ejercicio 2: Ondulaciones (SVG, Inkscape) |
| T34-ej2-ondulaciones.stl | Ejercicio 2: Ondulaciones (STL) |
| T34-ej3-monigote.fcstd | Ejercicio 3: Monigote (Freecad) |
| T34-ej3-monigote.svg | Ejercicio 3: Monigote (SVG, Inkscape) |
| T34-ej3-monigote.stl | Ejercicio 3: Monigote (STL) |
35 Calcando dibujos
| Video Tutorial 35/40 |
|---|
 Imagen de la llave. Bajada de internet. Créditos: deonildecasanova (click para ampliar) |
Descripción
Los dibujos en 2D se pueden extruir fácilmente en 3D, pero tenemos que tenerlos en formato SVG para poderlos editar con el Inkscape. Muhcas veces lo que tenemos son imágenes. Una opción es calcar esas imágenes. Colcamos la imagen a copiar en una capa de Inkscape, y en la capa superior dibujamos con rectas y curvas de bezier, calcando la imagen. Esto es muy útil para los que, como yo, no sabemos dibujar bien. Pero con el método del calcado sacamos unos dibujos chulísimos :-)
- Conceptos nuevos: capas en inkscape, importar imágenes, calcar imágenes
Explicación
Empezamos abriendo el menú de capas en el inkscape. Pinchamos en Layers / layers.... En la parte de la derecha cambiamos el nombre de la primera capa (Layer 1) a "imagen".
Pinchamos en el botón + que hay en el menú de capas. Se abre un diálogo y ponemos el nombre de la nueva capa. La llamamos "copia" porque es donde calcaremos la imagen de la capa inferior.
Seleccionamos la capa de la imagen y le damos a file/import para importar la nueva imagen. En el diálogo que aparece le decimos ok
Se abrirá la imagen. Hemos seleccionado la de una llave, para calcarla. Bloqueamos la capa de la imagen dándole al candado. De esta forma al pinchar sobre ella no se moverá.
Hacemos zoom, seleccionamos la herramienta para hacer líneas y curvas y empezamos a calcar la imagen.
Una vez terminado, no distinguiremos la línea nueva de la que hay debajo. Cambiamos el color de la línea a rojo. Para ello pinchamos en la parte inferior, donde están los colores y arrastramos el rojo a la casilla que pone "stroke".
Editamos la llave para ajustar todos sus puntos. Colocamos un círculo sobre el taladro de la llave
Pinchamos en el icono del ojo que hay delante de la capa de la imagen (en el menú de capas) para hacerla invisible. Ahora ya sólo veremos la capa con la copia de la imagen: la que hemos calcado. Finalmente la movemos al origen (esquina superior izquierda) y exportamos la llave a formato SVG plain (igual que hicimos en el tutorial anterior)
Abrimos el Freecad e importamos el fichero con el dibujo de la llave. Para hacer el taladro utilizaremos un cilindro. De esta manera podemos cambiar el radio y hacer el agujer paramétrico. Le damos al cilindro un radio que sea igual al del dibujo, y lo posicionamos encima. Bajamos su posición en z para que atraviese el boceto de la llave.
Extruimos la llave 5mm. Seleccionamos la llave, el cilincro y aplicamos una diferencia para hacer el taladro. ¡Ya tenemos nuestra llave!
Ejercicios propuestos
- Ejercicio 1: Logo python
- Ejercicio 2: Logo alianza rebelde
- Ejercicio 3: Logo obijuan academy
- Entregas de Jose Ignacio Alonso y Jaime Villegas
Créditos
- deonildecasanova es el autor del dibujo de la llave
Ficheros
| T35-ejemplo-llave.fcstd | Llave (Freecad) |
| T35-ejemplo-llave-1.svg | Llave (SVG) |
| T35-ejemplo-llave-2.svg | Llave (Plain SVG) |
| T35-ejemplo-llave.stl | Llave (STL) |
| T35-ej1-python-logo.fcstd | Logo de python (Freecad) |
| T35-ej1-logo-python.svg | Logo de python (SVG) |
| T35-ej1-logo-python-2.svg | Logo de python (Plain SVG) |
| T35-ej1-python-logo.stl | Logo de python (STL) |
| T35-ej2-rebel.fcstd | Logo de la alianza rebelde (Freecad) |
| T35-ej2-rebel.svg | Logo de la alianza rebelde (SVG) |
| T35-ej2-rebel-2.svg | Logo de la alianza rebelde (Plain SVG) |
| T35-ej2-Rebel.stl | Logo de la alianza rebelde (STL) |
| T35-ej3-obijuan-academy-logo.fcstd | Logo de la obijuan academy (Freecad) |
| obijuan-academy-logo1.svg | Logo de la obijuan academy (SVG) |
| obijuan-academy-logo2.svg | Logo de la obijuan academy (Plain SVG) |
| T35-ej3-obijuan-academy-logo.stl | Logo de la obijuan academy (STL) |
36: Poniedo texto!
| Video Tutorial 36/40 |
|---|
Descripción
El inkscape lo podemos utilizar para escribir mensajes de texto e importarlos luego en freecad, para extruirlos y poner texto y letras a nuestros diseños 3D. El texto en inkscape hay que convertirlo a trazos antes de exportar el fichero svg
- Conceptos nuevos: Texto en inkscape, convertir texto trazos
Explicación
Vamos a escribir texto en el inkscape. Pinchamos en el icono 
. Nos llevamos el puntero a la zona donde queremos poner el texto y hacemos click con el botón izquierdo. Escribimos el texto: "FREECAD". Le damos al icono 
para pasar el texto a negrita
Escalamos el texto. See puede escalar de varias maneras. Una es usando las flechas que hay alrededor del texto (al seleccionarlo). Pero siempre es mejor tener una noción real del tamaño, así que para ello nos vamos a la parte superior del menú y cambiamos las unidades de píxeles (px) a milímetros (mm). En las cajas superiores nos encontramos con una que poner W (witch) es la anchura total del texto y H (height) es la altura. Pinchamos en el icono del candado 
que hay entre ambas para mantener la proporción. Ponemos 40 en la caja W para que el texto sea de 40mm de ancho.
El texto tal cual se puede editar como si fuese texto normal. Lo siguiente es convertirlo a trazos. Le damos a la opción del menú path/objetct to path. Ahora al editar el texto ya no cambiamos las letras, sino que tenemos acceso a los puntos (somo si lo hubiésemos hecho nosotros mediante rectas y curvas de bezier).
Hacemos lo mismo que en los otros tutoriales: movemos el texto al origine, lo exportamos a SVG plano y lo importamos en Freecad. Seleccionamos todas las letras, bien en la parte de la izquierda (seleccionando el primero y luego el último pulsando shift) o bien en la ventana 3D dándole al shift-B y luego seleccionando con un cuadrado todo el texto.
Le damos el botón de extruir en el banco de trabajo part. Marcamos la casilla de objeto sólido y una distancia de por ejemplo 5mm.
El texto tiene algunas letras con la parte interior también extruida. Para eliminarlo hay que seleccionar la letra en cuestión, su interior y aplicar una diferencia. Empezamos por la R. La seleccionamos en la parte de la izquierda, junto con su interior. Hacemos la diferencia. Lo repetimos con el resto de letras que tienen hueco interior: A y D. Unimos todas las letras para tener un único objeto.
Hacemos la base de las letras. Lo podemos hace bien colocando un cubo y modificando sus dimensiones o haciendo un boceto. Elegimos este último. Creamos un rectángulo que contenga en su interior el texto y lo extruimos, por ejemplo 3mm.
Desplazamos el texto a lo largo del eje z para ponerlo encima de la base y lo unimos con el texto. Ahora tenemos un único objeto. ¡Listo para imprimir!
Ejercicios propuestos
- Ejercicio 1: Llavero con tu nombre
- Ejercicio 2: Letras hacia dentro
- Ejercicio 3: Bloques de letras
- Entregas de Jose Ignacio Alonso y Roberto Carlos Carmona
Ficheros
| T36-texto-freecad.fcstd | Texto "FREECAD" (Freecad) |
| T36-texto-freecad.svg | Texto "FREECAD" en inkscape (SVG) |
| T36-Texto-freecad.stl | Texto "FREECAD" (STL) |
| T36-ej1-llavero-nombre.fcstd | Ejercicio 1: Llavero con tu nombre (Freecad) |
| T36-ej1-llavero-nombre.svg | Ejercicio 1: Texto "OBIJUAN" (SVG) |
| T36-ej1-llavero-nombre.stl | Ejercicio 1: Llavero con tu nombre (STL) |
| T36-ej2-hola.fcstd | Ejercicio 2: Hola hacia dentro (Freecad) |
| T36-ej2-hola.svg | Ejercicio 2: Texto "HOLA" |
| T36-ej2-hola.stl | Ejercicio 2: Hola hacia dentro (STL) |
| T36-ej3-libre.fcstd | Ejercicio 3: Bloques de letras |
| T36-ej3-libre.svg | Ejercicio 3: Texto "LIBRE" |
| T36-ej3-bloque-letras.stl | Ejercicio 3: Hola hacia dentro (STL) |
37 Generando planos 2D
| Video Tutorial 37/40 |
|---|
Descripción
A partir de las piezas 3D podemos crear las proyecciones de las piezas y obtener los planos. Con Freecad 0.13 no se pueden poner cotas, pero sí podemos exportar el plano a un fichero SVG que luego podemos abrir con una aplicación externa para añadir cotas o información extra
- Conceptos nuevos: banco de trabajo drawing, Proyectar en un plano
Explicación
Vamos a sacar los planos de la rueda del miniskybot. Abrirmos el diseño 3D que ya tenemos hecho de otros tutoriales. Seleccionamos el banco de trabajo drawing. En los iconos superiores, pinchamos en el desplegable 
y seleccionamos el tamaño del plano: A4.
Nos aparecerá una carpeta llamada page. Hacemos doble click en ella y se nos abre una pestaña nueva en la zona del 3D llamada Drawing viewer. Vamos a crear las proyecciones de la pieza. Seleccionamos la rueda en la ventana de la izquierda (rueda-hueco-corona) y pinchamos en este icono 
para configurar las proyecciones.
Seleccionamos como vista primaria la frontal (front view). Nos aparece el frontal de la rueda en nuestro dibujo, en grande. La escala se calcula automáticamente para que se ajuste al tamaño de la hoja. En las vistas secundarias seleccionamos la superior (top) y la derecha (right). Esta última nos aparece encima del cajetín. La moveremos para ponerla encima.
Le damos al ok y dentro de la carpeta page seleccionamos la vista derecha (right). Nos vamos a la pestaña data. Modificamos la coordenada y para que valga 90. La vista derecha nos subirá. Ahora cambiamos la orientación de la pieza. Desplegamos el atributo direction y ponemos x = -1, z = 1.
Para cada proyección podemos cambiar el tamaño de las líneas, la rotación, la orientación, la posición, la escala y la visualización de las líneas ocultas.
Para la vista derecha vamos a visualizar las líneas ocultas y las "smooth lines". Ponemos esos atributos a true. Automáticamente se nos modifica el plano.
Finalmente seleccionamos la página en el árbol y le damos al icono 
para exportar el plano a un fichero .SVG. Para comprobar que está todo ok, lo abrimos con el inkscape. Podemos usar este programa además para añadir fácilmente texto. Rellenamos la caja inferior derecha con la información de la pieza
Ejercicios propuestos
- Ejercicio 1: Planos de la corona del servo
- Ejercicio 2: Planos del llavero con nombre
- Ejercicio 3: Planos del perfil de aluminio
- Entregas de Jose Ignacio Alonso y xxx
| [[|thumb|300px| (click para ampliar)]] | [[|thumb|300px| (click para ampliar)]] |
Ficheros
| T37-rueda-miniskybot.fcstd | Rueda del miniskybot, con los planos (Freecad) |
| T37-rueda-miniskybot-planos.svg | Planos de la rueda del miniskybot (SVG) |
| T37-ej1-corona-servo.fcstd | Corona del servo con los planos (Freecad) |
| T37-ej1-corona-servo.svg | Planos de la corona del servo (SVG) |
| T37-ej2-llavero-nombre.fcstd | Llavero con los planos (Freecad) |
| T37-ej2-Llavero-nombre.svg | Planos del llavero (SVG) |
| T37-planos/T37-ej3-perfil.fcstd | Perfiles de aluminio con los planos (Freecad) |
| T37-ej3-perfil.svg | Planos de los perfiles (SVG) |
38 Importando piezas en STL
| Video Tutorial 38/40 |
|---|
Descripción
Muchos de los objetos que nos encontramos en el mundo de la impresión 3D están en formato STL. Con Freecad los podemos importar, para visualizarlos. Pero también los podemos convertir a objetos nativos de Freecad y modificarlos. Para ello es neceario realizar una serie de conversiones.
- Conceptos nuevos: Importar STL, banco de trabajo mesh, convertir a objeto, convertir a objeto sólido, refinar un objeto
Explicación
En Freecad se pueden importar objetos en formato STL. Utilizaremos algunos de la Prusa Hephestos. Vamos a importar el carro del eje x. Le damos a la opción del menú file / import y seleccionamos el fichero .stl. Le damos a abrir y nos aparecerá en la ventana 3D. Podemos comprobar cómo NO lo podremos seleccionar desde la ventana 3D. Esto es porque NO es un objeto freecad, sino que es una malla. Por eso, en la ventana de la izquierda aparece junto al símbolo 
.
El banco de trabajo mesh nos permite trabajar con mallas: operaciones booleanas, análisis, reparaciones... pero no lo veremos aquí. Vamos a convertir la malla a un objeto freecad. Para ello le daremos a la opción "Create Shape from mesh..."
Nos aparecerá una ventana donde debemos indicar la tolerancia que queremos en la conversión. Dejamos el valor por defecto de 0.1mm. Nos aparece el objeto freecad. Hacemos invisible el objeto original. Vemos que el nuevo objeto tiene muchas líneas en sus caras. Son los triángulos que forman la malla.
Para eliminar esas líneas le damos a la opción del menú "part / refine shape". Sigue habiendo algunas líneas, sobre todo en las partes circulares. El software no las detecta como cilindros. Es parte de la información que se pierda al importar mallas. Nos falta un último paso que es hacer el objeto sólido. Nos vamos a la opción "Part / convert to solid". El nuevo objeto creado tendrá al final del nombre la cadena "(Solid)"
Ahora ya podemos trabajar con este objeto somo si lo hubiésemos creado de forma nativa en Freecad: podemos hacer operaciones booleanas, crear bocetos en sus caras, etc. Vamos a modificarlo para comprobarlo. Le vamos a poner nuestra inicial (o cualquier otro dibujo simple) grabado en una de sus caras. Nos vamos a part design, seleccionamos una cara y creamos un boceto.
Creamos la inicial de nuestro nombre. En mi caso una J. Cerramos el boceto y lo extruimos 0.5mm hacia fuera (pad). Ya tenemos la J en la pieza :-)
Vamos a hacer un vaciado en otra parte. Repetimos. Seleccionamos una cara y creamos un boceto. Hacemos un rectángulo
Lo extruimos hacia dentro para hacer el vaciado. Finalmente cambiamos la pieza de color. Hemos sido capaces de modificar una pieza que estaba en STL :-)
Ejercicios propuestos
- Ejercicio 1: Esquina del eje Y de la Prusa Hephestos modificada. Montaje parcial
- Ejercicio 2: Parte izquierda del eje X de la Prusa Hephestos modificada
- Ejercicio 3: Parte derecha del eje X de la Prusa Hephestos modificada. Montaje parcial
- Entregas de Jaime Villegas y Jose Ignacio Alonso
Ficheros
| T38-Carro-x-prusa-hephestos.fcstd | Prusa Hephestos: Carro x modificado (Freecad) |
| Prusa-hephestos-Carro-X.stl | Prusa Hephestos: Carro x original (STL) |
| Prusa-hephestos-Carro-X-modif.stl | Prusa Hephestos: Carro x modificado (STL) |
| T38-ej1-EjeY-esquina-prusa-hephestos.fcstd | Ejercicio 1: Esquina Eje Y montaje (Freecad) |
| Prusa-hephestos-EjeY_esquina.stl | Ejercicio 1: Esquina Eje Y original (STL) |
| Prusa-hephestos-EjeY_esquina-modif.stl | Ejercicio 1: Esquina Eje Y modificada (STL) |
| T38-ej2-EjeX-esquina-izquierda-Prusa-Hephestos.fcstd | Ejercicio 2: Pieza izquierda Eje x (Freecad) |
| Prusa-hephestos-EjeX_izquierda.stl | Ejercicio 2: Pieza izquierda Eje x original (STL) |
| Prusa-hephestos-EjeX_izquierda-modif.stl | Ejercicio 2: Pieza izquierda Eje x modificada (STL) |
| T38-ej3-EjeX-esquina-derecha-Prusa-Hephestos.fcstd | Ejercicio 3: Pieza derecha Eje x (Freecad) |
| Prusa-hephestos-EjeX_derecha.stl | Ejercicio 3: Pieza derecha Eje x original (STL) |
| Prusa-hephestos-EjeX_derecha-modif.stl | Ejercicio 3: Pieza derecha Eje x modificada (STL) |
39 Intercambiando datos en formato STEP
| Video Tutorial 39/40 |
|---|
Descripción
El formato STEP es un estándar internacional para el intercambio de datos en la industrial. Permite que las piezas diseñadas con una aplicación determinada se exporten a step y que luego se puedan importar en otra aplicación diferente. Freecad puede importar/exportar ficheros en formato step. Esto es muy útil porque los fabricantes de elementos mecánicos (tornillos, tuercas, rodamientos, etc.) suelen dar los diseños 3D en step para así poderlos incluir en nuestras piezas.
- Conceptos nuevos: formato step, importar step, exportar step
Explicación
Como ejemplo de importar un fichero step vamos a descargar el modelo 3D del móvil bq Aquaris 5.7, disponible en este enlace: Aquaris step files. También está disponible en la sección de descargas de este tutorial.
Para importar un fichero step en Freecad, nos vamos al menú file / import. En el selector de ficheros, donde pone "supported formats" indicamos que queremos importar un fichero del tipo "STEP WITH COLORS". Marcamos el fichero bq_Aquaris_5_7.stp y le damos a open. Se nos abrirá el 3D dl aquaris. Observamos que, a diferencia de cuando se importan objetos STL, aquí el objeto ya es un objeto Freecad. Se pueden seleccionar sus caras como las de cualquier otro objeto de Freecad.
Creamos un boceto en el plano xy, con un rectángulo que tenga el teléfono en su interior y lo extruimos 14mm
El teléfono sobresale por la parte inferior. Lo desplazamos hasta la posición Z = 7 para que sobresalga un poco por la parte superior
Seleccionamos la cama, luego el teléfono y aplicamos una diferencia. Obtenemos la cama. Vamos a ponerle unas aberturas laterales para poder sacar el teléfono. Seleccionamos la superficie superior.
y creamos un boceto nuevo en ella. Hacemos dos rectángulos que pasen por encima de los laterales del teléfono. Los hacemos simétricos. Las dimensiones las ponemos a ojo (por ser un ejemplo)
En perspectiva se aprecian mejor los nuevos rebajes. Ahora redondeamos las cuatro aristas verticales de la cama.
Cambiamos el color de la cama, para resaltarla y hacemos una copia del aquaris para ponerlo encima, de ejemplo.
Cambiamos los colores al Aquaris, para que la pantalla sea negra y la carcasa blanca. Por último desplazamos el aquaris en el eje z, para que se vea el interior de la cama y el teléfono. Ya sabemos cómo importar ficheros STEP con los modelos 3D y diseñar piezas nuevas a partir de ellos :-)
Ejercicios propuestos
- Ejercicio 1: Soporte para aquaris 5.7
- Ejercicio 2: Viendo los detalles de la impresora 3D witbox
- Ejercicio 3: Despiece del hotend de la Witbox
- Entregas de Ruben Nieves López y xxxxxx
| [[|thumb|300px| (click para ampliar)]] | [[|thumb|300px| (click para ampliar)]] |
Ficheros
| bq_Aquaris_5_7.stp | Móvil bq aquaris 5.7 (STEP) |
| bq-aquaris-5-7.fcstd | Móvil bq aquaris 5.7 (Freecad) |
| T39-aquaris-5-7-cama.fcstd | Cama para el Aquaris 5.7 (Freecad) |
| T39-aquaris-5-7-cama.stl | Cama para el Aquaris 5.7 (STL) |
| T39-ej1-soporte-aquaris-5-7.fcstd | Soporte para el Aquaris 5.7 (Freecad) |
| T39-ej1-soporte-aquaris-5-7.stl | Soporte para el Aquaris 5.7 (STL) |
| witbox-hotend.stp | Hotend de la witbox (STEP) |
| T39-ej3-witbox-hotend.fcstd | Hotend de la witbox despiezado (Freecad) |
40 Despedida: Que el software libre os acompañe
| Video Tutorial 40/40 |
|---|
Descripción
¡¡Fin de la temporada!! ¡¡Muchas gracias a todos!! y... que el software libre os acompañe
Ejercicio propuesto
- Comparte tus diseños con licencias libres :-)
Tomas falsas
- Toma falsa del tutorial 3. Me parto el cubo
Participantes
- Tutoriales: 40
- Ejercicios propuestos: 102
- Total de entregas recibidas: 457
- Ejercicios enviados:
| Jose Ignacio Alonso | 87 |
| Emilio Jose Morán Hevia | 84 |
| Bedelber JC | 76 |
| Jose Raul Montero Ponce | 58 |
| Alfonso López | 31 |
| JV Almodovar | 24 |
| Rubén Nieves López | 21 |
| Jose del Valle | 14 |
| Roberto Carlos Carmona | 15 |
| Carlos Cervilla | 8 |
| Jose Maria Martin | 6 |
| Jose Luis V. | 6 |
| Jaime Villegas | 6 |
| Xoan Sampaiño | 5 |
| Fernando Remiro | 4 |
| Federico Coca | 3 |
| Mizael Galvez | 2 |
| Adolfo Castaño | 2 |
| Miguel Angel de Frutos | 1 |
| Antonio Javier Lucas | 1 |
| Jakolete | 1 |
| Ricardo Perez | 1 |
| Francisco Pons ruiz | 1 |
Diseños recibidos
Estos son algunos de los diseños que han hecho las personas que han seguido este tutorial. ¡Gracias!
- Drift Trike, por Lucas Aaron Ruggiero (Argentina)
 Drift_Trike_v2.0.FCStd (click para ampliar) |
- Florero, por Francisco Malpartida (España)
- Perfil de Ala y soporte de motor, por Carlos Cervilla (España)
- Tuercas y Escudo del capitán américa, por Roberto Carlos Carmona
- Jaula para insectos, por Jose Ignacio Alonso
- Portalápices, por Alberto Valero
- Panel de Abeja, por Rafael Lorenzo
- Printrbot simple (versión metal), por Jose Hevia
- Soporte Hotend intercambiable, por Antonio Navarro
- Prisma pentagonal con torsión impreso por Ruben Nieves López:
Muro homenaje
El 17 de Junio de 2014, Federico Coca, de Granada Imprusa, publicó este post en G+ con las fotos del muro homenaje a obijuan :-) ¡Me hizo una ilusión tremenda! ¡Gracias Federico!
Esta es la cabecera del muro:
Y este es el muro, con todas las piezas que se han hecho en el tutorial. ¡Grande, muy grande Federico!
Repositorio
Los ficheros fuentes están en este repositorio:
Autor
- Juan González (Obijuan)
Licencia
 This work is licensed under a Creative Commons Attribution-ShareAlike 2.5 Spain License.
|
Sobre este tutorial
Este tutorial está realizado exclusivamente usando herramientas libres.
|
Enlaces
Otros tutoriales de Freecad
- Tutorial. Wiki de Spainlabs
- Tutoriales de Christian Herencia: Tutorial 1 (español)
- Tutoriales de Bejant: Tutorial 1 (Inglés)
- Tutoriales de MarthamEngineering: tutorial 1 (Inglés)
- Tutoriales de BPLRFE: tutorial 1 (Alemán)
- Canal de 61quick en Youtube: 61quick (Inglés). Tiene un montón de vídeos que son una pasada
Otros enlaces
Documentación
- Manual oficial de referencia de Freecad
- Linuxforanengineer: Blog con cantidad de información sobre Freecad
Bibliotecas de piezas
- BOLTS: Biblioteca libre de piezas técnicas
- Freecad Library: Biblioteca de objetos
Noticias
- 14/Julio/2014: Publicado el vídeo de despedida. Temporada I terminada! ¡Gracias!
- 2/Julio/2014: Normand Chamberland, moderador de la comunidad de Freecad en G+, publica este post donde menciona los tutoriales y agradece el trabajo. ¡Gracias Normand! :-)
- 17/Junio/2014: Federico Coca publica el muro homenaje ¡Gracias! :-)
- 27/Abril/2014: Aparecen los tutoriales en la página principal de Freecad
- 30/Marzo/2014: Comenzada esta página
|
|
Proyecto Clone wars: Construye tu impresora 3D opensource! |
 |
Proyecto RepRap: Impresoras 3D auto-replicantes. El origen de la revolución de las impresoras 3D opensource |
 |
Obijuan Academy, Tu academia rebelde! ;-) |
