Category: robotica

El otro día Yossua fue retado a un duelo, se celebrará en Campus Party 2008. El culpable TupperBot de Mif.

Por eso Yossua está buscando zaparos nuevos. Por ahora esto es lo que ha encontrado.

Andrés

El programa que estoy usando para hacer los dibujos de mi tesis es el Inkscape. Es un programa de dibujo en 2D, libre y multiplataforma (Linux, Mac, Windows). Lo mejor es que los ficheros se graban en el formato vectorial SVG, que es abierto y basado en XML.
Yo descubrí este programa el año pasado, cuando acudí a la iParty9 en Castellón de la Plana. Desde entonces lo estoy usando.

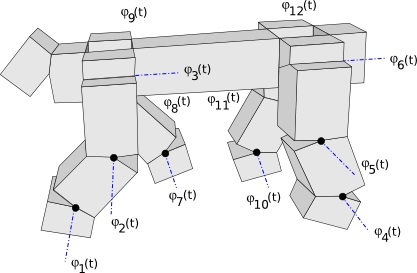
Nunca he sido un buen dibujante, pero con el inkscape puedo hacer muy fácilmente dibujos como este robot cuadrúpedo modular que he dibujado hoy. La técnica es muy sencilla. A partir de una foto o pantallazo lo único que tienes que hacer es importarla en inkscape y “calcarlo”, igual que hacíamos en prescolar

El cuadrúpedo lo he “calcado” de esta imagen que he geneado con el MRSuite.

Obijuan

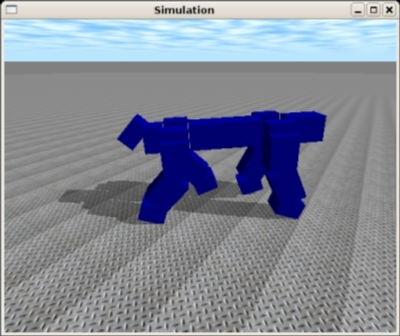
Bueno, aquí he dejado un video, un poco mejor que el anterior. Esta claro que en casa de herrero cuchillo de palo.

[youtube]http://www.youtube.com/watch?v=o5idMjOk0DQ[/youtube]

Andrés

Aprovechando el mal tiempo que acompaña estos días, pero que nos viene de maravilla, he construído el FlatBot. Se trata de una especie de Skybot (lleva las misma electrónica), pero con una base plana y grande para poder poner un portátil encima.

El portátil se comunica con la Skypic para controlar los motores, y nosotros a su vez, podemos conectarnos el portátil mediante Bluetooth o WiFi. De esa forma tenemos una plataforma móvil controlada por nuestro PC y siendo muy fácil la programación de algoritmos complejos.

Otra aplicación de moda e interesante es controlar el robot con el mando de la Wii como se ve en este video. El cámara es tan friki que lo ha grabado girado, mañana os subo uno mejor.

Andrés

Minicube-3 es la configuración mínima con topología de 2 dimensiones. Se puede desplazar en tres direcciones diferentes y rotar en sentido horario y antihorario.

Aquí se puever el robot movíendose hacia adelante y atrás:

[youtube]http://www.youtube.com/watch?v=-J9Q5GOh5lQ[/youtube]

Y aquí está rotando en sentido horario y antihorario:

[youtube]http://www.youtube.com/watch?v=JJXtEeyaelw[/youtube]

Obijuan

Minicube-2 es la configuración mínima de tipo “gusano” (topología 1D) que se puede desplazar en un plano. Está formada sólo por 3 módulos Y1, pero al menos puede realizar cinco tipos de movimientos:
* Desplazamiento en línea recta
* En arco
* Desplazamiento lateral
* Rotaciones paralelas al suelo
* Rodar

Lo mejor es ver el robot en acción:

[youtube]http://www.youtube.com/watch?v=SpLH-hHXigg[/youtube]

Y claro, no podía faltar la versión FRIKI

[youtube]http://www.youtube.com/watch?v=v_iHzKmxNjw[/youtube]

Obijuan

Un problema muy interesante es el de las configuraciones mínimas. ¿Cuál es el mínimo número de módulos necesarios para realizar la locomoción de un robot modular en 1 y 2 dimensiones?. Así fue como nació Minicube.

En entradas previas he hablado sobre los robots Cube Revolutions e Hypercube ambos de 8 módulos que pueden moverse en 1 y 2 dimensiones respectivamente. Si nos centramos en la locomoción en una dimensión, ¿Cuántos módulos necesitamos para que el robot se pueda desplazar? ¿8?, ¿7?, ¿3?, ¿1?…¿? La respuesta es 2.

En este vídeo se puede ver la locomoción de Minicube, compuesto únicamente por dos módulos Y1 que se mueven perpendicularmente al suelo.

[youtube]http://www.youtube.com/watch?v=EK6Pqhsq7kY[/youtube]

Y muchos diréis, “Vale, mola, es muy chulo… pero ¿Para qué vale?” Yo he estudiado este problema con estos objetivos en la cabeza:

Estudio de la coordinación en 1D.

Aprender un poco más sobre coordinación para conseguir locomoción. La manera en que se coordinan los servos para producir este moviento se puede aplicar a configuraciones mayores. Digamos que Minicube-1 contiene la “esencia del movimiento”

Maximizar el número de partes en que se puede dividir un robot modular auto-configurable. Un robot modular de M módulos, podrá dividirse como máximo en M/2 mini-robots de 2 módulos cada uno. Cada uno de estos mini-robots podrá desplazarse en línea recta.

El segundo punto es muy interesante. Imaginemos que hay una tubería recta (sin curvas) situada horizontalmente. Esta tubería por ejemplo puede estar conduciendo gas o puede ser un conducto de ventilación. Se ha producido un escape o ha aparecido algún tipo de microorganismo que queremos detectar. Una solución es introducir un robot modular de tipo gusano que recorra el tubo en busca del problema (el escape de gas o la bacteria).

Solución “centralizada”: Que el robot recorra el tubo desde un extremo al otro.

Otra solución: En vez de que el gusano analice el tubo secuencialmente, se podría dividir en M/2 minirobots, cada uno de ellos explorará una zona. Ahora el problema se está resolviendo de una forma “distribuida”. Una vez finalizada la tarea, los M/2 robots se podrán volver a juntar en un único robot.

Si el robot tiene 12 módulos, ¿Cuántos mini-robots como máximo se podrían tener? Como sabemos que la configuración mínima es de 2 módulos, la solución es fácil: 6 mini-robots. Luego el diseñador de la aplicación puede decidir si utilizar estos 6 mini-robots o un número menor: 4 de tres módulos, 2 de 6, etc… Pero nunca más de 6, o de lo contrario no se podrán desplazar.

Obijuan

Últimamente llevo mucho tiempo encerrado en casa escribiendo la tesis… y tengo que dar rienda suelta a mi frikismo o exploto:

[youtube]http://www.youtube.com/watch?v=GUuVUEFfbEg[/youtube]

Obijuan

Sigo con los experimentos de mi tesis. Ahora le ha tocado el turno a Hypercube, un robot modular de 8 módulos que construí para estudiar el problema de la locomoción en un plano. Al menos puede realizar los siguientes desplazamientos:

Adelante y atrás

Trayectorias en arco para realizar giros

Desplazamiento lateral

Rotaciones paralelas al suelo

Rodar

En este vídeo se muestran todos los tipos de movimientos:

[youtube]http://www.youtube.com/watch?v=RJL-buxNiD4[/youtube]

y en este otro algunas pruebas de giros:

[youtube]http://www.youtube.com/watch?v=41KzBiw7LvM[/youtube]

Obijuan

He terminado de subir todos los vídeos que tenía de Cube Revolutions a Youtube. Así los tengo controlados y no se me pierden.

No puedo dejar de mencionar una de las pruebas más frikis que hice. Esta es la prueba de que los sistemas linux son estables:

[youtube]http://www.youtube.com/watch?v=AIpi2DtrvdU[/youtube]

Como se puede ver, NO SE CAE

Otro vídeo clásico es de Cube haciendo la cobra:

[youtube]http://www.youtube.com/watch?v=2q9zxepYLtM[/youtube]

y en su versión más friki, adoptando la forma del logo de Debian:

[youtube]http://www.youtube.com/watch?v=ijcbWqJUxGA[/youtube]
(Eso fue sugerido por Alvaro López [Yosh])

Y también está friki-cube. Con un par de calcetines como funda…

[youtube]http://www.youtube.com/watch?v=zTkq-v0_XSo[/youtube]